Deep Q Learning (DQN)

reinforcement learning deep learning

!!! กรุณาอ่าน Q learning ก่อน

List of Variable and Function

Deep Q-learning คืออะไร

Deep Q-learning คือ Q-learning ที่ใช้ neural network มาประมาณค่า Q แทนที่จะเก็บค่า Q ทุกค่าในตาราง

ถ้าใครยังจำกันได้ ใน Q learning คือเราพยายามจะประมาณค่า \(Q(s,a)\) ของทุก state และ action และเก็บค่า Q นั้นลงในตาราง ซึ่งวิธีนี้มันก็มีข้อจำกัดอยู่หน่อย (ที่จริงก็ไม่หน่อย) ก็คือมันใช้ได้กับแค่ปัญหาที่มีจำนวน state จำกัด อย่างเช่น FrozenLake-v0 ในบทความที่แล้วเท่านั้น ซึ่งเป็นไปได้ยากในโลกแห่งความเป็นจริง ลองคิดดูว่าสมมติเราจะนำ Q learning ไปขับรถ สมมติเราตั้งให้ state เป็นภาพจากกระจกหน้ารถ ซึ่งภาพจากกระจกหน้ารถนั้นจะเป็นอะไรก็ได้ ซึ่งก็แปลว่าจำนวน state นั้นมีมหาศาลเลย แล้วเราจะสร้างตารางมาเก็บมันยังไงหมด

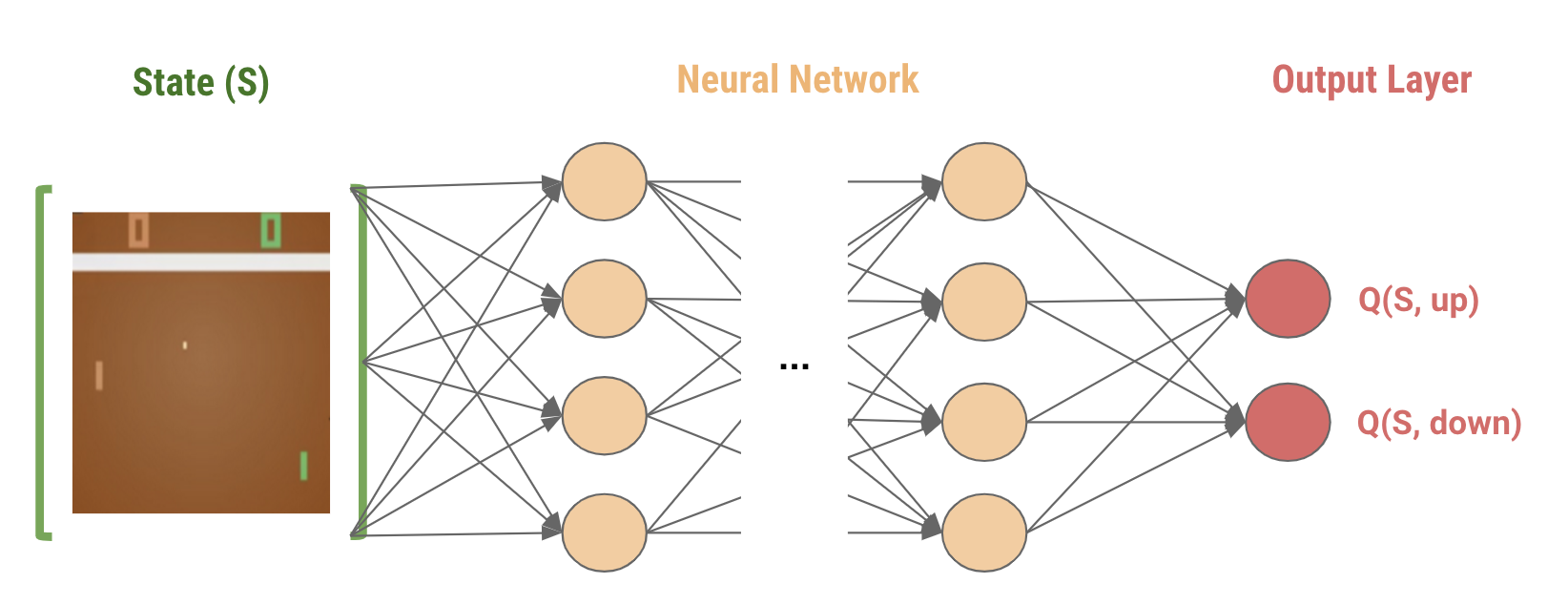
ซึ่งนักวิจัยเค้าก็เลยเสนอให้เราใช้ neural network ในการประมาณค่า \(Q(s,a)\) แทน โดยที่ neural network นั้นจะรับ state เข้าไปเป็น input และทำนายค่า \(Q(s,a)\) ของแต่ละ action บนแต่ละ node ของ state แทน

alt text

Loss Function

เหมือนกับใน supervised-learning คือการอัพเดท neural network ใน DQN นี้เราก็จะต้องทำ gradient descent บน loss function ระหว่างค่าจริงกับค่า predict

โดยที่ใน DQN นั้น loss function จะเป็น mean squared error ระหว่าง

ซึ่งก็คือ เราสามารถเขียน loss function ได้ในรูปแบบนี้

\begin{equation} \label{eq:loss} (r_t + \gamma max_{a} Q(s_{t+1},a; \theta) - Q(s_t,a_t; \theta))^2 \end{equation}

จะเห็นได้ว่าการคิด loss จะต้องประกอบไปด้วย 4 ตัวแปร ก็คือ \(\{s_t,a_t,r_t,s_{t+1}\}\) ซึ่งเราจะเรียกเซ็ตนี้ว่า experience

ขั้นตอนการเทรน neural network เพื่อประมาณค่า Q

ขั้นตอนโดยหลัก ๆ แล้วก็จะคล้ายคลึงกับใน Q-learning ก็คือ การปล่อยให้ agent เราได้ interact กับ environment และในแต่ละ timestep มันจะเก็บ experience หรือ \(\{s_t,a_t,r_t,s_{t+1}\}\) มาเพื่ออัพเดทค่า Q

alt text Ref: Playing Atari with Deep Reinforcement Learning

แต่จะมีจุดแตกต่างกันดังนี้ คือ ใน Deep Q Learning นั้นเรามีการใช้เทคนิคที่ชื่อว่า Experience Replay ซึ่งจะช่วยทำให้เราเทรน neural network ได้อย่างมีประสิทธิภาพ

Experience Replay

เทคนิค experience replay โดยคร่าวคือ แทนที่จะใช้แค่ experience จาก timestep ล่าสุดมาอัพเดทค่า Q value ผู้คิดค้น DQN เสนอให้เก็บ experience ล่าสุดลงใน memory แล้วเราค่อยสุ่มหยิบ experience ใน memory มาซักชุดนึงเพื่อมาอัพเดท neural network

การทำแบบนี้มีข้อดี 2 ประการด้วยกัน

  1. Sample-Efficient กว่า หรือก็คือ experience นึงหรือ sample นึงนั้น สามารถถูกสุ่มหยิบมาใช้อัพเดท neural network ได้หลายครั้ง
  2. ถ้าเราเอาแต่ experience ล่าสุดไปอัพเดท neural network สิ่งที่เกิดขึ้นคือ experience ที่ติด ๆ กันจะมี correlation กัน ซึ่งจะทำให้เราเทรน neural network ได้ไม่มีประสิทธิภาพ การที่เราเก็บ experience ลงใน memory แล้วค่อยสุ่มหยิบมั่ว ๆ นั้นจะช่วยตัด correlation ระหว่างข้อมูลที่นำเข้าไปเทรน neural network ได้

จากวิธีการ experience replay เราสามารถเขียน loss function ได้ใหม่ดังด้านล่าง ซึ่งหมายความว่า loss function เราคือ expected value ของ loss function ในสมการที่ \eqref{eq:loss} โดยที่คิดมาจาก experience ที่ sample มาจาก memory \(\mathcal{D}\)

\begin{equation} \label{eq:loss_exp_rpl} E_{(s,a,r,s’) \sim U(\mathcal{D})} [(r + \gamma max_{a} Q(s’,a; \theta) - Q(s,a; \theta))^2] \end{equation}

Target Network

คำถามต่อมาคือ การที่เราจะอัพเดท \(\theta\) ด้วย loss function ในสมการที่ \eqref{eq:loss_exp_rpl} ถือว่ามันโอเครึยัง คำตอบคือมันก็โอเคในระดับหนึ่ง แต่ที่จริงแล้วมันยังซ่อนปัญหาอีกปัญหานึงไว้ ซึ่งปัญหานั้นเกิดจากการที่เราใช้ \(\theta\) เดียว ในการคำนวณทั้งค่า

และในทุกครั้งที่เราอัพเดทตัวแปร \(\theta\) เพื่อขยับ \(Q(s,a;\theta)\) เข้าไปให้ใกล้ \((r + \gamma max_{a} Q(s',a; \theta)\) มากยิ่งขึ้น แต่เพราะว่าค่าของ \(\theta\) มันเปลี่ยน มันก็เลยเหมือนกับเราเผลอไปขยับค่า \((r + \gamma max_{a} Q(s',a; \theta)\) ออกไปโดยไม่รู้ตัว

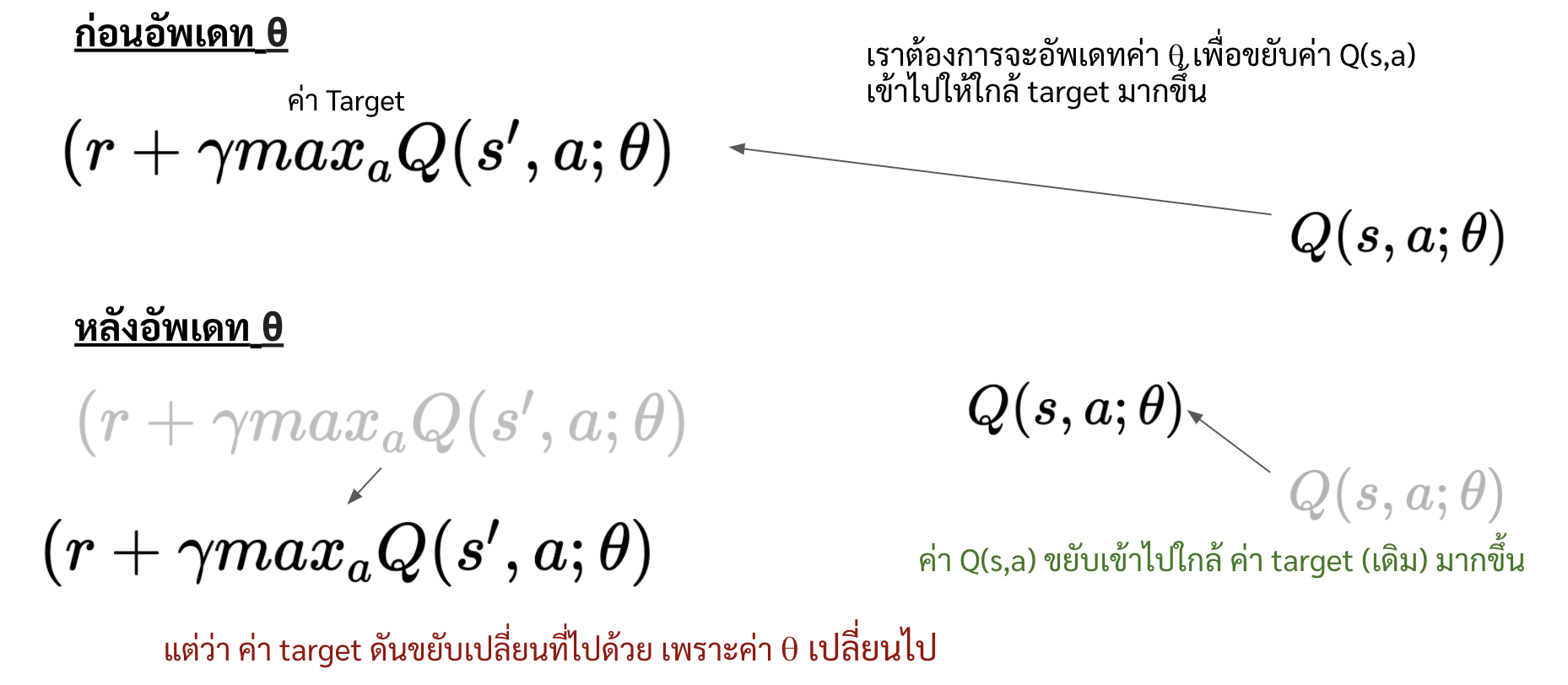
alt text

วิธีบรรเทาปัญหานี้คือการสร้าง neural network ที่เหมือนกันขึ้นมา 2 ชุด ได้แก่

เพราะฉะนั้น เราสามารถเขียน loss function ได้ใหม่ดังนี้

\begin{equation} \label{eq:loss_target_network} E_{(s,a,r,s’) \sim U(\mathcal{D})} [(r + \gamma max_{a} Q(s’,a; \theta^-) - Q(s,a; \theta))^2] \end{equation}

โดยที่ในการเทรนโมเดลแต่ละครั้งนั้น เราจะอัพเดทเฉพาะ \(\theta\) และในทุก ๆ ช่วงที่กำหนดไว้ เราจะก๊อปค่า \(\theta\) ไปใส่ให้ \(\theta^-\) ดังแสดงใน pseudo-code ด้านล่าง

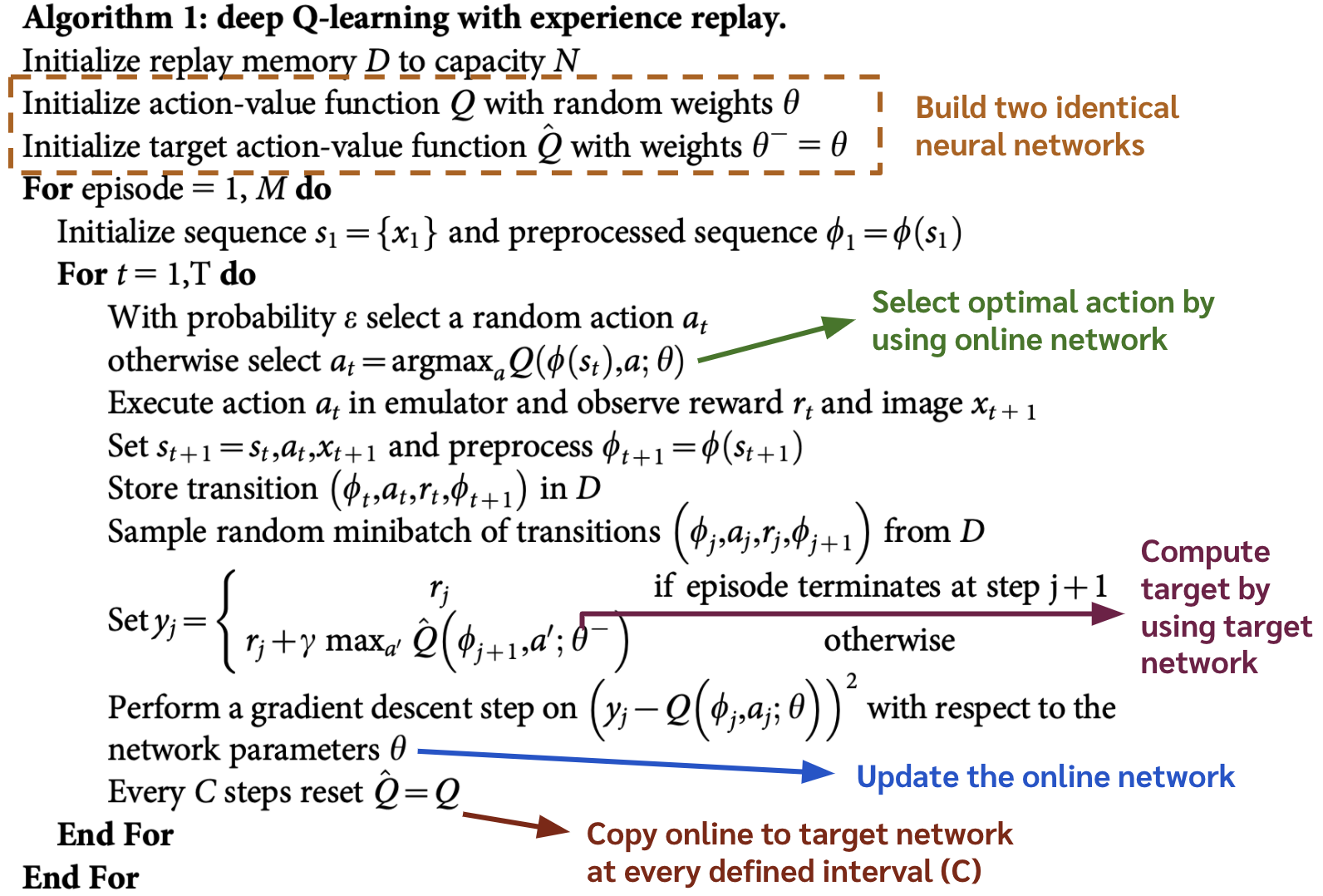alt textRef: Human-level control through deep reinforcement learning

แต่ที่จริงแล้วมีวิธีอัพเดทค่า \(\theta^-\) อีกวิธีหนึ่งที่ชื่อว่า soft-update ซึ่งจะค่อย ๆ เปลี่ยนค่า \(\theta^-\) ไปเรื่อย ๆ โดยที่ เราจะตั้งค่า \(\tau\) ไว้ ซึ่งมักจะตั้งให้เป็นค่าน้อย ๆ ่เช่น 0.001 แล้วเราจะอัพเดทค่า \(\theta^-\) ในทุก ๆ timestep ด้วยสมการด้านล่าง

\begin{equation} \label{eq:soft_update} \theta^- = (\tau)\theta + (1-\tau)\theta^- \end{equation}

Implementation

ในส่วนนี้จะพาทุกท่านมาเขียนโค้ด DQN อย่างง่ายกัน โดยเราจะใช้ library แค่ numpy และ keras เป็นหลักเท่านั้น

อธิบาย Environment

ในบทความนี้จะยกตัวอย่างการใช้ DQN ในการบังคับยานลงจอดในเกม LunarLander-v2

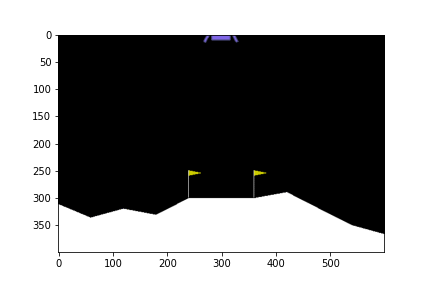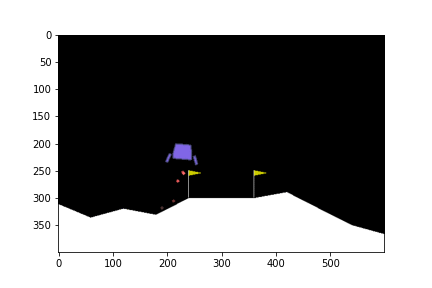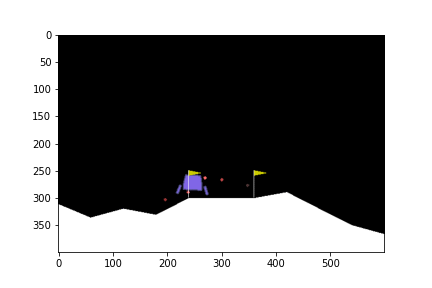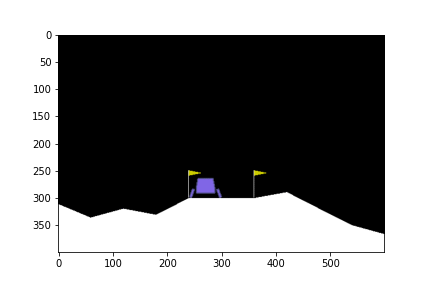
State ใน environment นี้ประกอบด้วยตัวเลข 8 ตัวด้วยกัน ซึ่งก็คือ

Action มี 4 actions ด้วยกัน ได้แก่

ปล. ที่จริงแล้ว เราไม่จำเป็นต้องรู้ว่า state คืออะไร และแต่ละ action คืออะไรก็ทำได้

โดยที่ Reward ใน environment นี้จะคิดดังนี้

Coding

โค้ดทั้งหมดสามารถทำได้บน google colab โดยที่ตามไปก๊อปได้จาก notebook นี้เลยครับ

  1. ก่อนอื่นเรามาสร้าง Environment และเช็ค shape ของ observation และจำนวน action 
     import gym
 env = gym.make('LunarLander-v2')
 print ('Observation Space: ',env.observation_space) # ได้ 8
 print ('Action Space: ',env.action_space) # ได้ 4

  2. สร้าง neural network ด้วย keras ในขั้นตอนนี้ถ้าใครอยากสร้าง neural network แบบไหนก็ได้เลย แต่โดยส่วนตัวคิดว่า environment นี้มันไม่ยากมาก ก็ใช้ fully connected แค่ 2 layers ก็น่าจะพอ

     from tensorflow.keras.layers import Input, Dense
 from tensorflow.keras import Model
 from tensorflow.keras.optimizers import Adam
 def build_neural_network():
   input_layer = Input(shape=(8,)) #input shape เอามาจาก env.observation_space 
   dense = Dense(100, activation='relu', kernel_initializer='random_normal')(input_layer)
   dense = Dense(100, activation='relu', kernel_initializer='random_normal')(dense)
   output = Dense(4, activation='linear', kernel_initializer='random_normal')(dense) #จำนวน output node เอามาจาก env.action_space
   model = Model(input_layer,output) 
   adam = Adam(learning_rate = 0.001)
   model.compile(loss='mean_squared_error', optimizer=adam) # ตั้ง loss value เป็น mean squared error
   return model
 # สร้าง neural network ที่หน้าตาเหมือนกัน 2 ชุด คือ onine กับ target network
 online_network = build_neural_network()
 target_network = build_neural_network()

  3. ตั้งพารามิเตอร์สำหรับเทรน DQN

     memory_size = 100000
 reward_discount_factor = 0.99
 number_of_ep = 1000
 epsilon = 1.0
 epsilon_decay_factor = 0.999
 epsilon_min = 0.01
 batch_size = 32
 target_network_update_int = 500

  4. สร้าง memory เปล่า ๆ ที่เอาไว้เก็บ experience ด้วย deque

     from collections import deque
 memory = deque(maxlen=memory_size)

    เหตุผลที่ใช้ deque เพราะเวลาเราเพิ่ม experience เข้าไปใน memory จนเกิน mexlen ที่ตั้งไว้ มันจะลบ experience ที่เก่าที่สุดทิ้ง ซึ่งทำให้ experience ใน memory นั้นมาจาก policy ที่ไม่เก่ามาก (อย่าลืมว่าเวลาเราเทรน DQN ไปเรื่อย ๆ ค่า Q เปลี่ยน ทำให้ policy เปลี่ยน แล้วพอ policy เปลี่ยนไป ก็จะมีผลต่อ experience ด้วย เพราะทำให้ในแต่ละ state อาจจะเลือก action ไม่เหมือนเดิม)

  5. โค้ดในการเทรน DQN ทั้งหมดจะเป็นแบบนี้

     from tqdm.notebook import tqdm # เอาไว้สร้าง progress bar ว่าเทรนไปกี่ ep แล้ว
 import pickle
 import numpy as np
 import random
 ## สร้าง List เอาไว้เก็บประวัติ reward รวมของแต่ละ ep เพื่อดูการพัฒนา
 reward_hist = []
 t = 0
 for ep in tqdm(range(number_of_ep+1)):
   state = env.reset()
   reward_of_ep = 0
   while True:
     ## เลือก action ด้วย epsilon greedy
     optimal_action = np.argmax(online_network.predict(state.reshape(1,8))[0])
     random_action = random.randint(0,env.action_space.n-1)
     action = np.random.choice([random_action,optimal_action],p=[epsilon,1-epsilon])
     ## ทำ action ใส่ environment
     next_state,reward,done,_ = env.step(action)
     ## เก็บ experience ลงใน memory
     memory.append([state,action,reward,next_state,done])
     ## รอให้เก็บ experience ให้ได้ตาม batch size ก่อน
     if len(memory)>=batch_size:
       ## สุ่มหยิบ experience จาก memory มา batch นึง
       batch = np.array(random.sample(memory, batch_size))
       ## หาค่า target
       target = batch[:,2] + reward_discount_factor*(np.max(target_network.predict(np.stack(batch[:,3])),axis=1)) * (1-batch[:,4])
       ## หาค่าพรีดิกในปัจจุบัน
       current_Q = target_network.predict(np.stack(batch[:,0]))
       ## สร้าง target ซึ่งเป็นการแทนที่ค่า Q(s,a) ของ experience ด้วยค่า target ที่คำนวณมา 
       current_Q[np.arange(batch_size),list(batch[:,1])] = target
       ## Fit model
       online_network.fit(np.stack(batch[:,0]), current_Q, verbose=False)
     ## ก้าวไป next state
     state = next_state
     ## ลดค่า epsilon
     if epsilon>epsilon_min: epsilon = epsilon*epsilon_decay_factor
     ## รวมค่า reward_of_ep (เอาไว้ดูเฉยๆ)
     reward_of_ep += reward
     ## ในทุก ๆ ช่วง target_network_update_int ให้อัพเดท target network
     if t%target_network_update_int==0:
       target_network.set_weights(online_network.get_weights())
     t += 1
     ## ถ้าสิ้นสุด episode แล้วก็ให้ออกจาก loop นี้ ไปเริ่ม episode ถัดไป
     if done:
       break
   reward_hist.append(reward_of_ep)
   ## Save model เอาไว้ดูผลในภายหลัง
   if ep%20==0:
     online_network.save('drive/My Drive/Blog/DQN/model/{}.h5'.format(ep))
     pickle.dump(reward_hist,open('drive/My Drive/Blog/DQN/score.pkl','wb'))

    เพื่อความไม่งงจะขอหยิบโค้ดส่วน fit model มาอธิบายเพิ่มเติมแล้วกันนะครับ

     ## สุ่มหยิบ experience จาก memory มา batch นึง
 batch = np.array(random.sample(memory, batch_size))
 ## หาค่า target
 target = batch[:,2] + reward_discount_factor*(np.max(target_network.predict(np.stack(batch[:,3])),axis=1)) * (1-batch[:,4])
 ## หาค่าพรีดิกในปัจจุบัน
 current_Q = target_network.predict(np.stack(batch[:,0]))
 ## สร้าง target ซึ่งเป็นการแทนที่ค่า Q(s,a) ของ experience ด้วยค่า target ที่คำนวณมา 
 current_Q[np.arange(batch_size),list(batch[:,1])] = target
 ## Fit model
 online_network.fit(np.stack(batch[:,0]), current_Q, verbose=False)

    โดยที่เดี๋ยวจะขอยกตัวอย่างง่าย ๆ ให้ดูแทนที่จะเป็น lunarlander แล้วกันนะครับ

    • ก่อนอื่นเราต้องสุ่มเลือก experience มาจาก memory จำนวนเท่ากับ batch_size

        batch = np.array(random.sample(memory, batch_size))

      ซึ่งเราจะได้ตารางของ experience มาโดยที่ แต่ละ row คือ แต่ละ experience และ column คือ state, action, reward, done

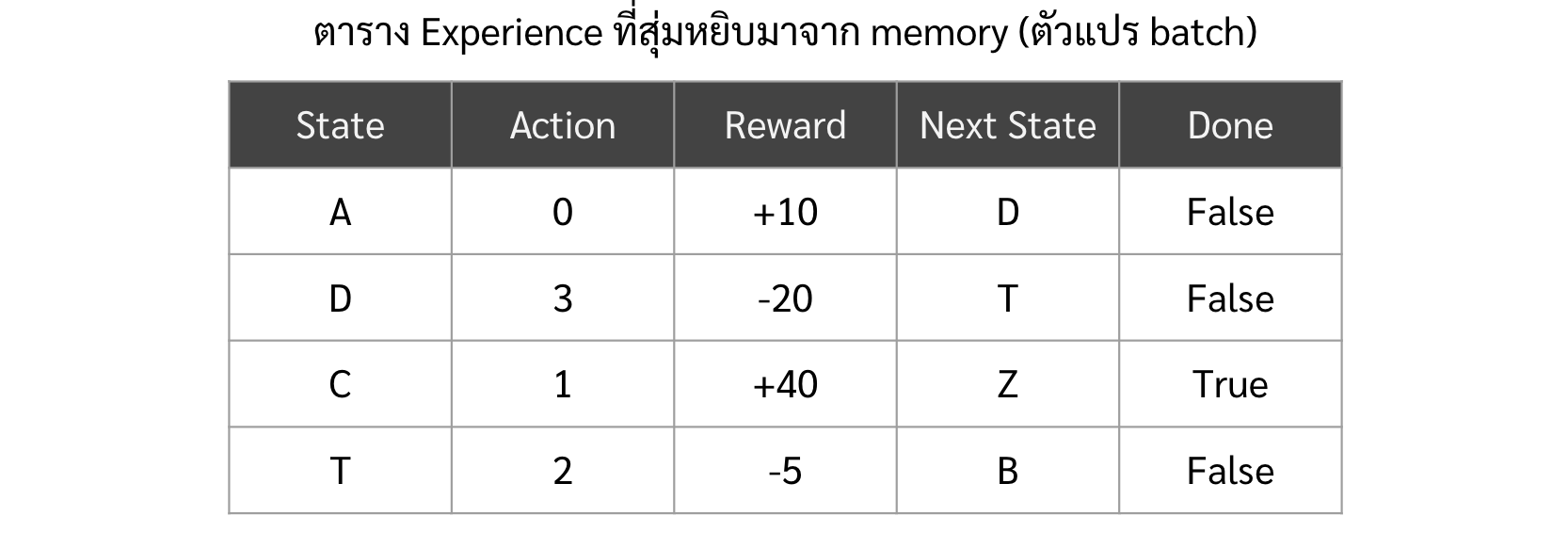
      alt text

    • แล้วเราก็หาค่า target ของ Q(s,a) ของแต่ละ experience

        target = batch[:,2] + reward_discount_factor*(np.max(target_network.predict(np.stack(batch[:,3])),axis=1)) * (1-batch[:,4])

      ถ้าเทียบกับใน pseudo code คือทำอันนี้

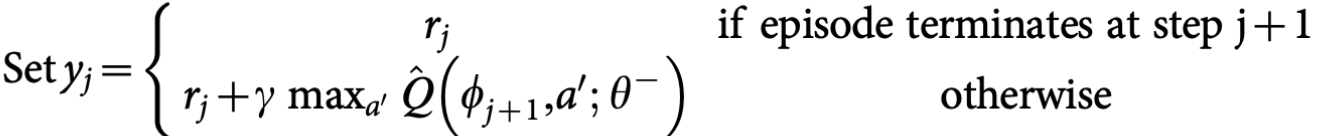
      alt text

      จะเห็นได้ว่า เราใช้วิธีคูณด้วย (1-batch[:,4]) แทนที่จะแยกเคสเหมือนใน pseodo code โดยที่ batch[:,4 คือ list ของค่า boolean ที่บอกว่า episode จบลงหลัง experience นั้นหรือไม่ (True คือจบ, False คือยังไม่จบ)

      เราสามารถกระจายขั้นตอนนี้ออกมาโดยละเอียดได้ดังนี้

      • ก่อนอื่น เอา next state ไปเข้า neural network และหาค่า max ของ Q(s’,a) ออกมาก่อน 
          ...np.max(target_network.predict(np.stack(batch[:,3])),axis=1)) * (1-batch[:,4])...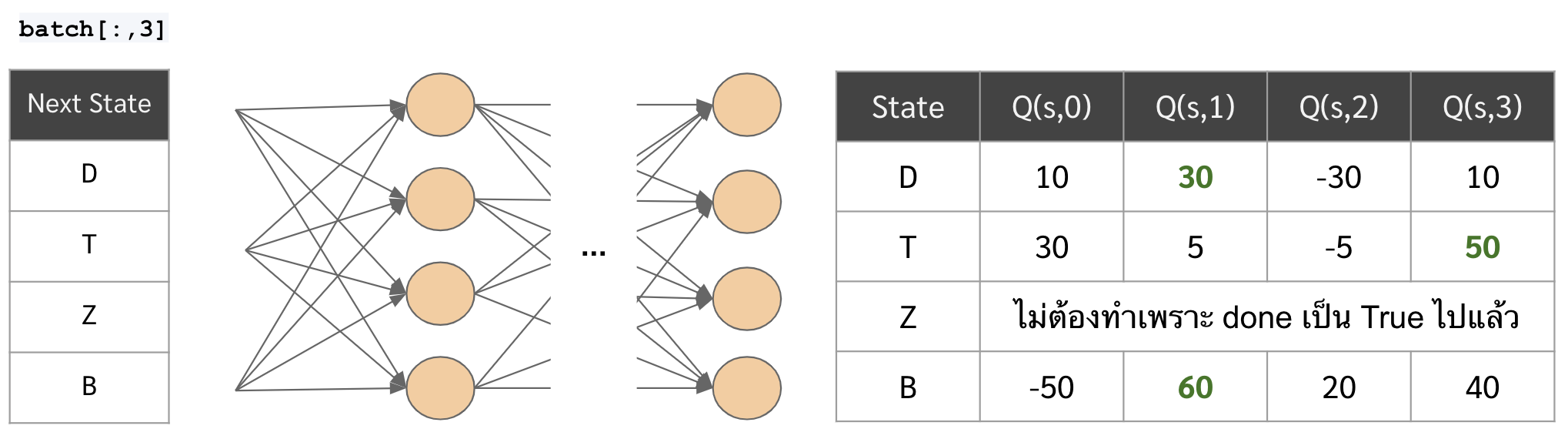

        alt text

      • ต่อมาเอาค่า max ของ Q(s’,a) มารวมกับ reward เพื่อสร้างเป็นค่า target value ตามสูตร Bellman Equation
        **หมายเหตุ รูปด้านล่างสมมติให้ reward discount factor เป็น 0.9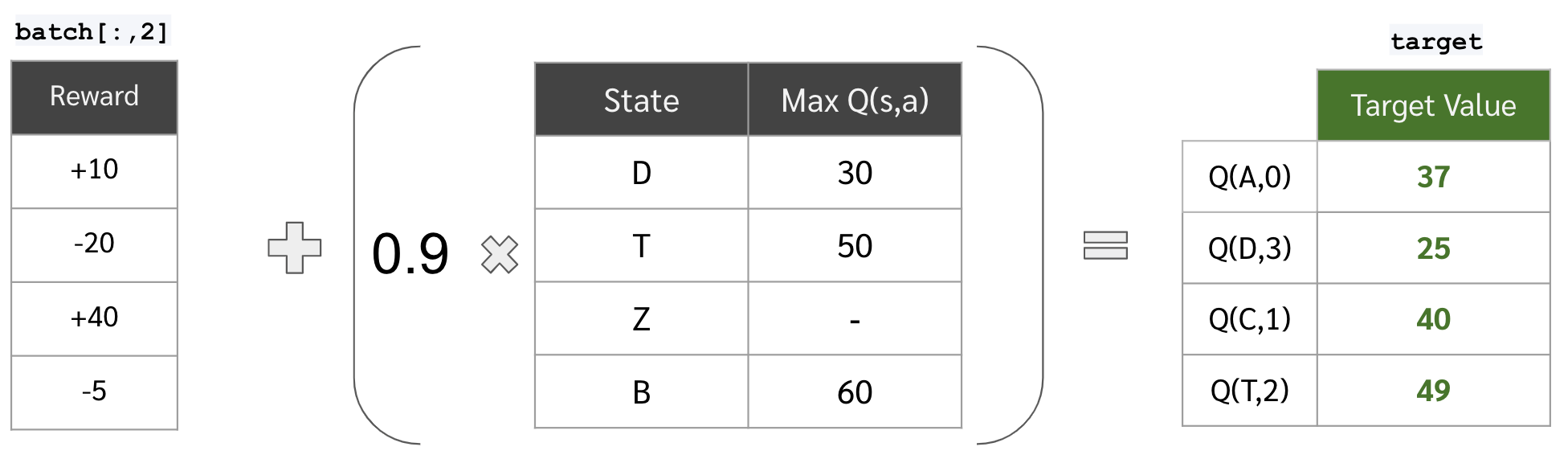

        alt text

    • ต่อมาเราต้องสร้างตารางของค่า target เพื่อเอาไป fit กับ model โดยที่ในตารางนั้นจะต้องมีครบทั้ง Q(s,a) ของทุก action แต่ว่าค่า target ที่เราหามาตะกี้ เราเพิ่งมีแค่ของ action เดียว (ซึ่งก็คือ action ที่อยู่ใน experience) เราเลยจะใช้ค่า Q(s,a) เดิมของ action อื่น ๆ เป็นค่า target ไปก่อน โดยที่ขั้นตอนมีดังนี้
      • หาค่า Q(s,a) ของ state ในแต่ละ experience 
          current_Q = target_network.predict(np.stack(batch[:,0]))

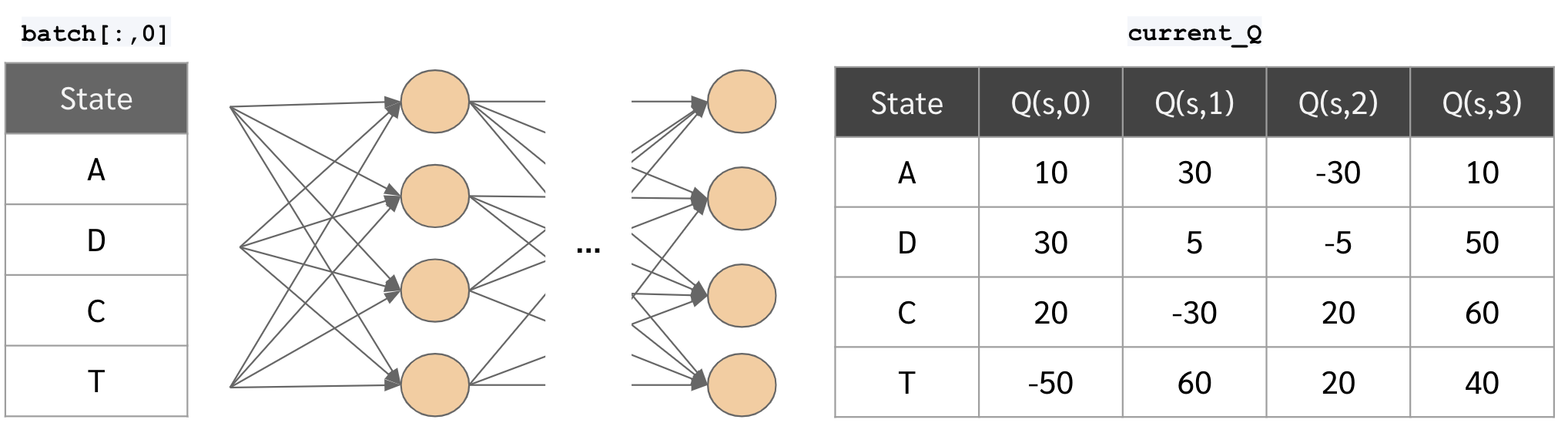
      alt text

      • แทนที่ค่า Q(s,a) ของ action ใน experience ด้วยค่า target ที่เราหามาในข้อก่อนหน้า 
          current_Q[np.arange(batch_size),list(batch[:,1])] = target

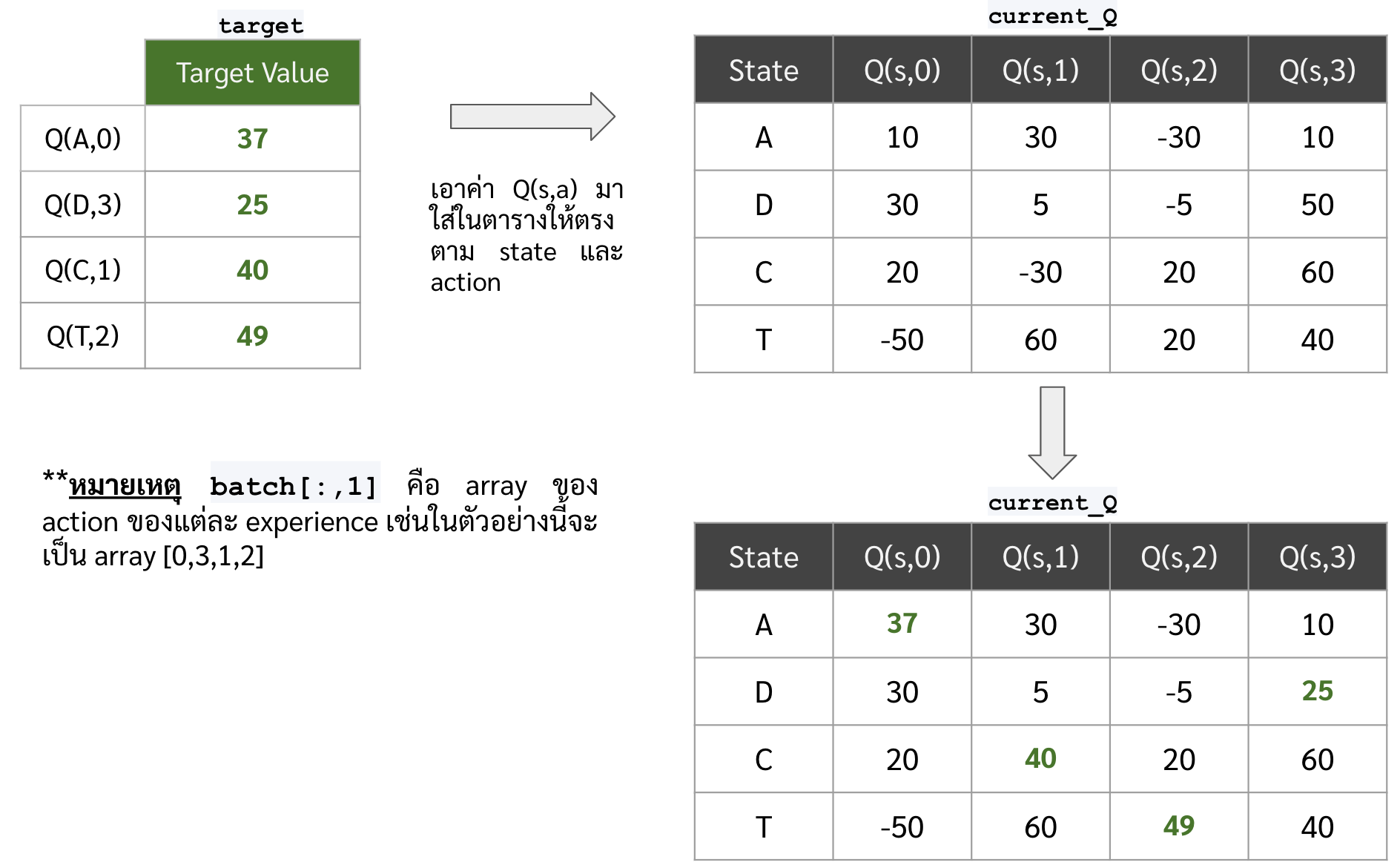
      alt text

    • เอาตารางค่า Q(s,a) ที่ได้มา ไปเทรน online network

        online_network.fit(np.stack(batch[:,0]), current_Q, verbose=False)
Result

พล็อตดูพัฒนาการของ reward รวมของแต่ละ episode กัน จะเห็นได้ว่าแนวโน้ม reward รวมที่ได้รับในแต่ละ episode นั้น จะดีขึ้นเรื่อย ๆ

import matplotlib.pyplot as plt
plt.figure(figsize=(10,5),dpi=200)
plt.plot(reward_hist)
plt.xlabel('Episode')
plt.ylabel('Reward')

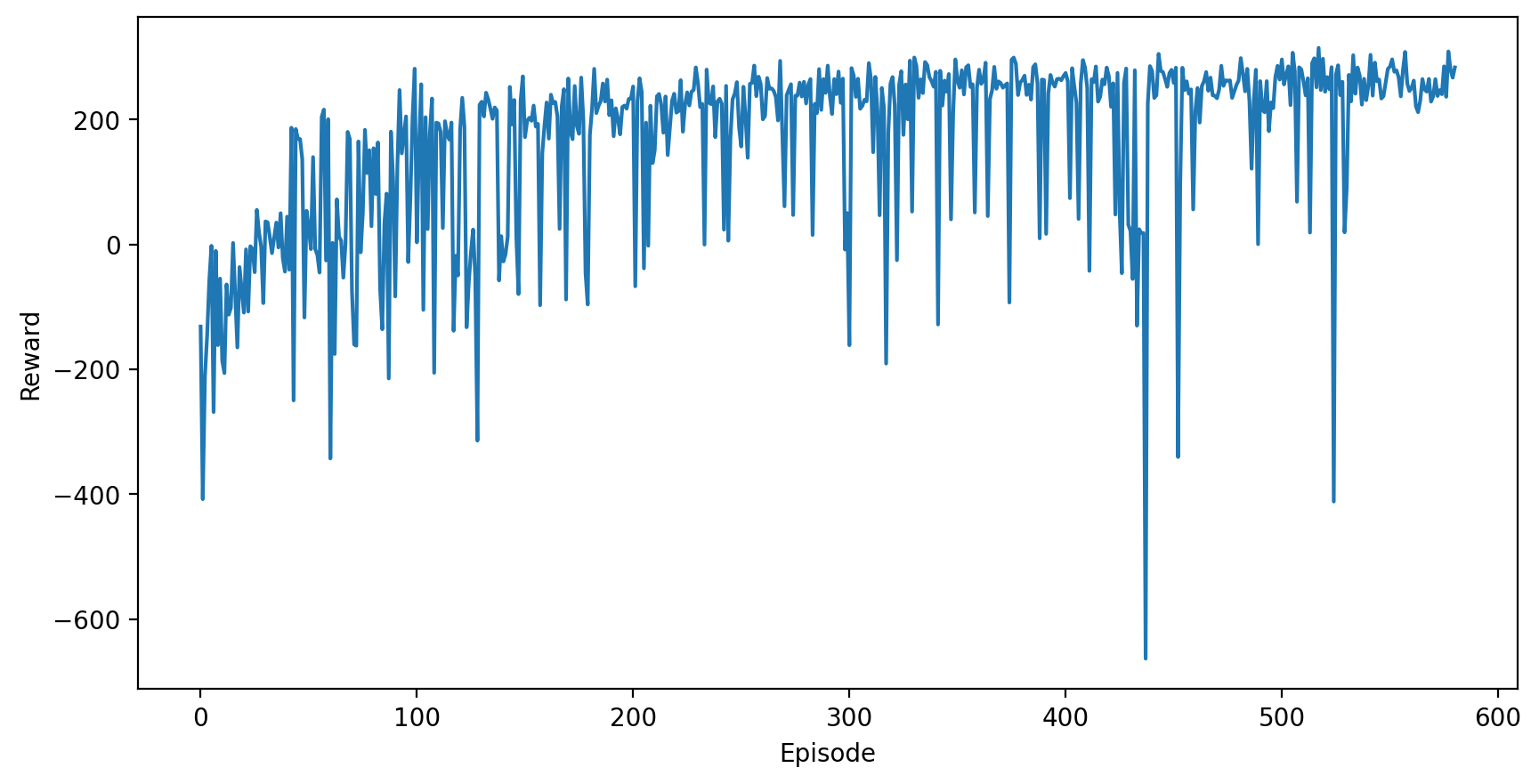
alt text

ดูกันว่าเมื่อเทรนไปเรื่อย ๆ แล้วยานลงจอดได้แบบไหนกันบ้าง

ปล. โค้ดในการทำ VDO หรือไฟล์ gif อยู่ใน notebook ที่แปะไว้ให้นะครับ

0 episode
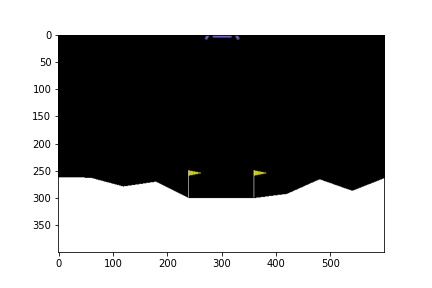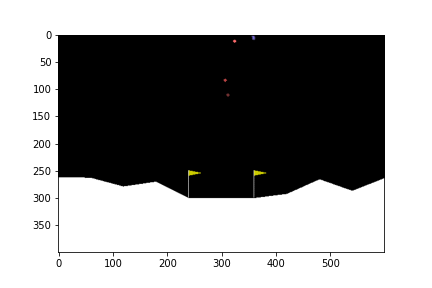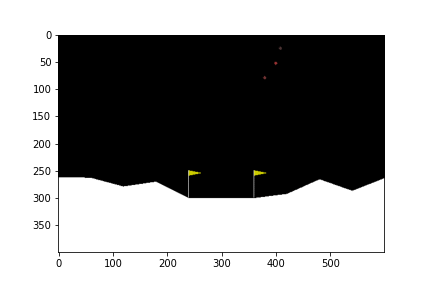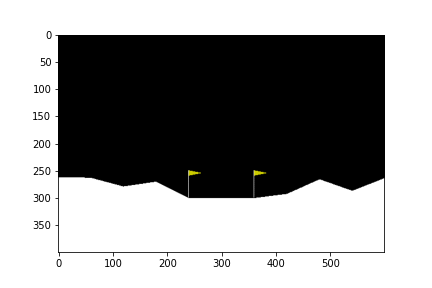
Bootstrap Image Preview
100th episode
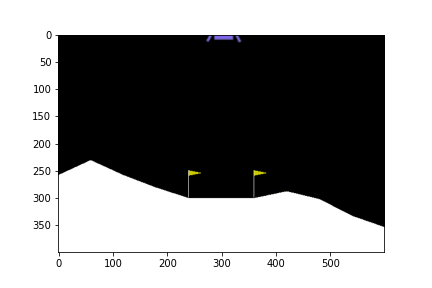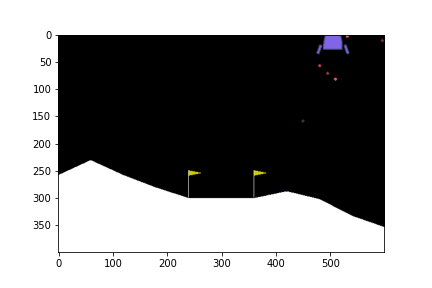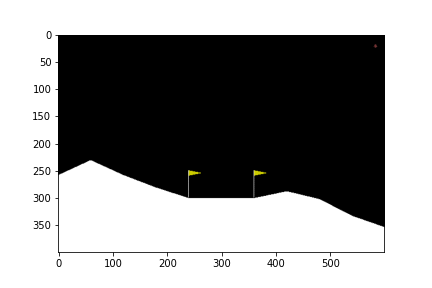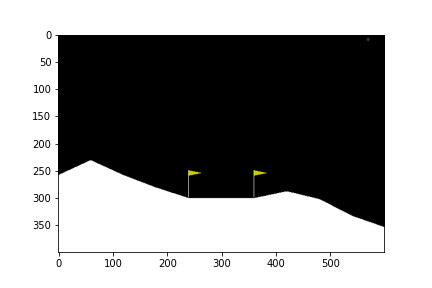
Bootstrap Image Preview
300th episode
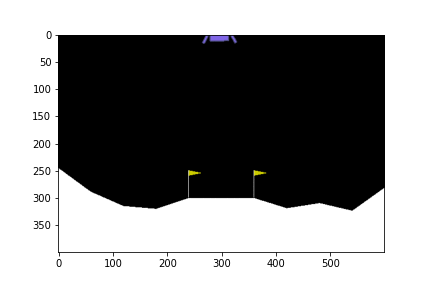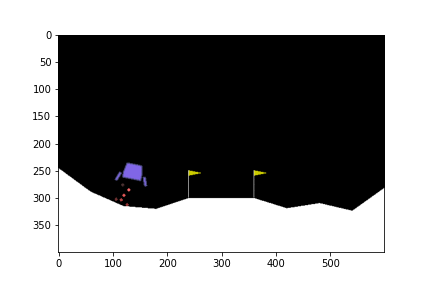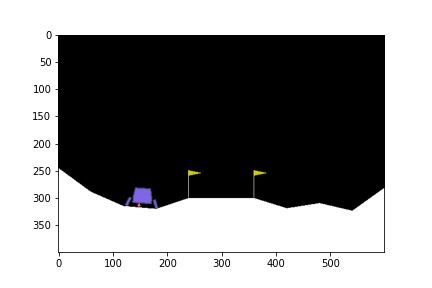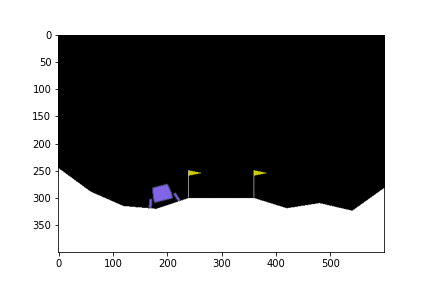
Bootstrap Image Preview
500th episode
Bootstrap Image Preview

จะเห็นได้ว่าในตอนแรกนั้น ยานยังลงจอดเองไม่ได้ด้วยซ้ำ บินหายไปไหนไม่รู้เลย แต่เมื่อให้มันเรียนรู้จากการพยายามลงจอดไป 300 รอบ มันก็เริ่มลงจอดได้ แต่ว่ายังไม่ตรงจุด (ไม่ลงตรงกลางระหว่างธง) จนมันฝึกลงจอดไปครบ 500 รอบมันถึงเริ่มขยับเข้ามาจอดตรงกลางได้

Reference: