!!! กรุณาอ่าน PDP plot ก่อน

เมื่อบทความก่อนหน้า เราพูดถึง Partial Dependence Plot (PDP) กันไปแล้ว ซึ่งเป็นวิธีพื้นฐานที่ใช้ดู insight ว่าแต่ละค่าของฟีเจอร์มีผลอย่างไรกับ output ของ model บ้าง แต่จริง ๆ แล้ว PDP นั้นยังมีปัญหาสำคัญอีกหนึ่งอย่างด้วยกัน คือ การที่มันเก็บซ่อนความสัมพันธ์ในทางตรงกันข้ามกัน (heterogenouse effect) ในฟีเจอร์เดียวไว้ ในบทความนี้เลยจะมาแนะนำให้รู้จักกับ Individual Conditional Expectation plot หรือตัวย่อคือ ICE plot นั่นเอง

ICE Plot คือ

เอาแบบสั้น ๆ เลย ICE plot ก็คือ PDP แบบที่ไม่ได้เอาไป average กัน แต่ plot โชว์ทุกเส้นไปเลย ถ้าใครจำไม่ได้ว่า PDP มันทำยังไงก็ไปทบทวนบทความ PDP ก่อนเนอะ พอดีเป็นคนเขียนอธิบายไม่ค่อยเก่ง เลยทำรูปข้างล่างมาให้แล้วจ้า

ทำไมเราถึงควรดู ICE plot

เพื่อที่จะทำให้เห็นภาพได้ชัดยิ่งขึ้นจะขอเกริ่นถึงปัญหาที่ PDP มีอยู่ก่อน ใน PDP นั้นตัวที่ทำให้เกิดปัญหาเลยคือการหาค่าเฉลี่ยแล้วค่อย plot เนื่องจากการทำเช่นนั้นจะทำให้มันซ่อน heterogeneous effect ได้อย่างหมดจด  heterogeneous effect คือความสัมพันธ์แบบตรงข้ามกัน ยกตัวอย่างเช่น ผู้ป่วยชนิดหนึ่งทานยา A แล้วอาการจะดีขึ้น แต่ผู้ป่วยอีกชนิดหนึ่งทานยา A แล้วจะแย่ลง ถ้าเราใช้ partial dependence plot ฟีเจอร์การทานยา A ออกมาดู ตัว PDP นั้นจะเฉลี่ยค่าที่ดีขึ้นและแย่ลงกลายเป็นค่ากลาง ๆ แล้วค่อยแสดงให้เราดู ทำให้เรารู้สึกว่าการทานยา A ไม่ได้มีผลทั้งดีขึ้นและแย่ลงต่อผู้ป่วยเลย

ซึ่งจะเห็นได้ว่า heterogeneous effect นั้นมาจากการที่มันมีตัวแปรอื่น ๆ ที่เราอาจจะไม่รู้หรือไม่ได้สนใจมาบังคับทิศทางของความสัมพันธ์ระหว่างตัวแปรอื่น ๆ กับค่าที่โมเดลทำนายออกมา ตัวอย่างใน paper ที่นำเสนอ ICE plot [1] ยกตัวอย่างให้ดูนั้น เค้าลองสร้างชุดข้อมูล regression ด้วยสมการด้านล่าง

สมการ

จะเห็นได้ว่าสมการประกอบไปด้วย 3 features (X1, X2, X3)และ 1 target value (Y) นอกจากนี้จะสังเกตได้ว่าความสัมพันธ์ระหว่าง X2 กับ Y นั้นมีผลตรงกันข้ามกันอย่างสิ้นเชิงเมื่อ X3>0 และ <0 และเมื่อเค้าลองเอาข้อมูลที่เค้า gen ขึ้นมาไปเทรนโมเดล regression แล้วพล็อต PDP ของ X2 ออกมาตามรูปด้านล่างก็พบว่ามันเป็นเส้นตรงเรียบซะนิ่งเลย ถามว่าฟีเจอร์ X2 ไม่มีผลอะไรกับผลการทำนายเลยรึเปล่า คำตอบก็ต้องไม่ใช่อยู่แล้ว ฟีเจอร์ X2 นี่มีผลเต็ม ๆ กับค่า Y เลย แค่มันโดนควบคุมด้วยฟีเจอร์ X3 อยู่ด้วย

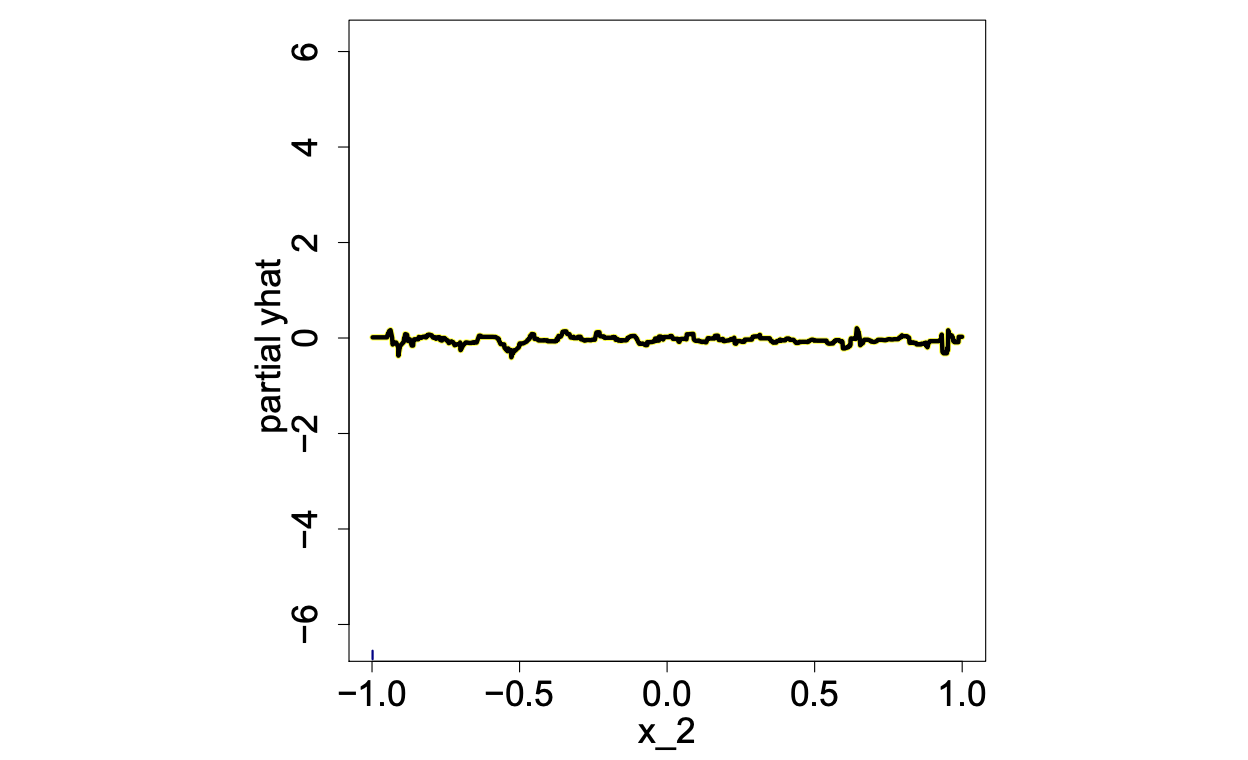
เหล่าผู้คิดค้น ICE plot ก็เลยปิ๊งไอเดียเพื่อมาแก้ปัญหาแบบง่าย ๆ ว่า เราก็ไม่ต้อง average มันสิ ก็พล็อตมันทุกเส้นไปเลย หรือถ้ามันเยอะไปก็ sample มาพล็อตเอาก็น่าจะได้เห็นอะไรบ้าง ก็เลยเกิดเป็นรูป ICE plot ด้านล่าง ทีนี้เราจะเห็นว่าข้อมูลมันแบ่งเป็น 2 กลุ่ม ก็จะทำให้เกิดการ explore ต่อไปมีฟีเจอร์อื่นใดที่สามารถแบ่งทิศทางความสัมพันธ์ระหว่างฟีเจอร์ X2 และค่า Y ได้ (ซึ่ง ณ ที่นี่เรารู้กันอยู่แล้วว่าคือ X3)

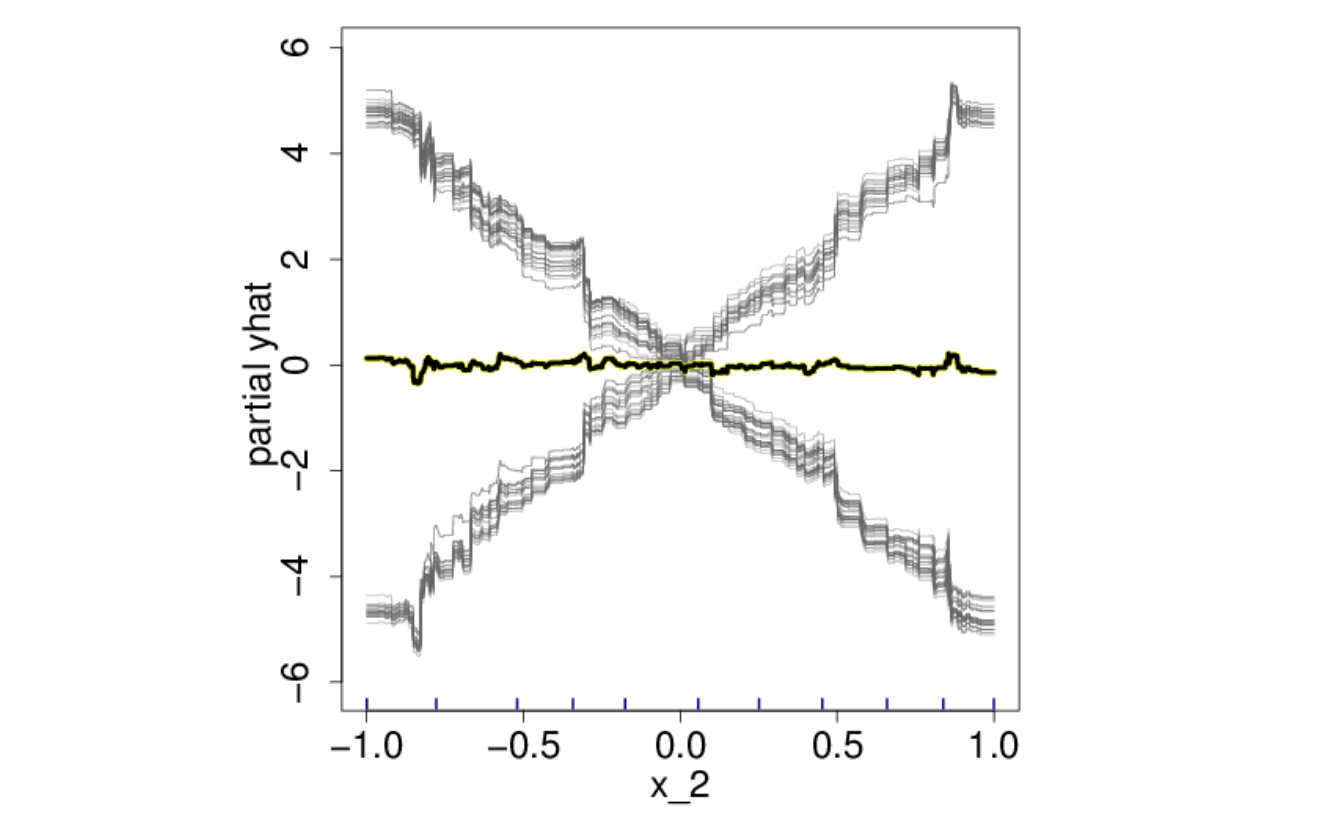
Centered ICE (c-Ice) plot

เอาจริง ๆ การพล็อต ICE plot ธรรมดามันก็แอบดูยากนิดนึง (ลืมรูปบนไปก่อนนะ รูปนั้นมันดูง่ายเพราะว่า dataset มัน perfect) ยกตัวอย่างในเปเปอร์นั้นเค้าทำ ICE plot ของ boston house dataset ออกมา มันได้รูปนี้ (ปล. boston house dataset เป็น dataset ที่เอาไว้ทำ regression เพื่อทำนายราคาบ้านจากฟีเจอร์ต่าง ๆ เช่นอายุบ้าน จำนวนห้องนอน ห้องครัว ตำแหน่ง ฯลฯ)

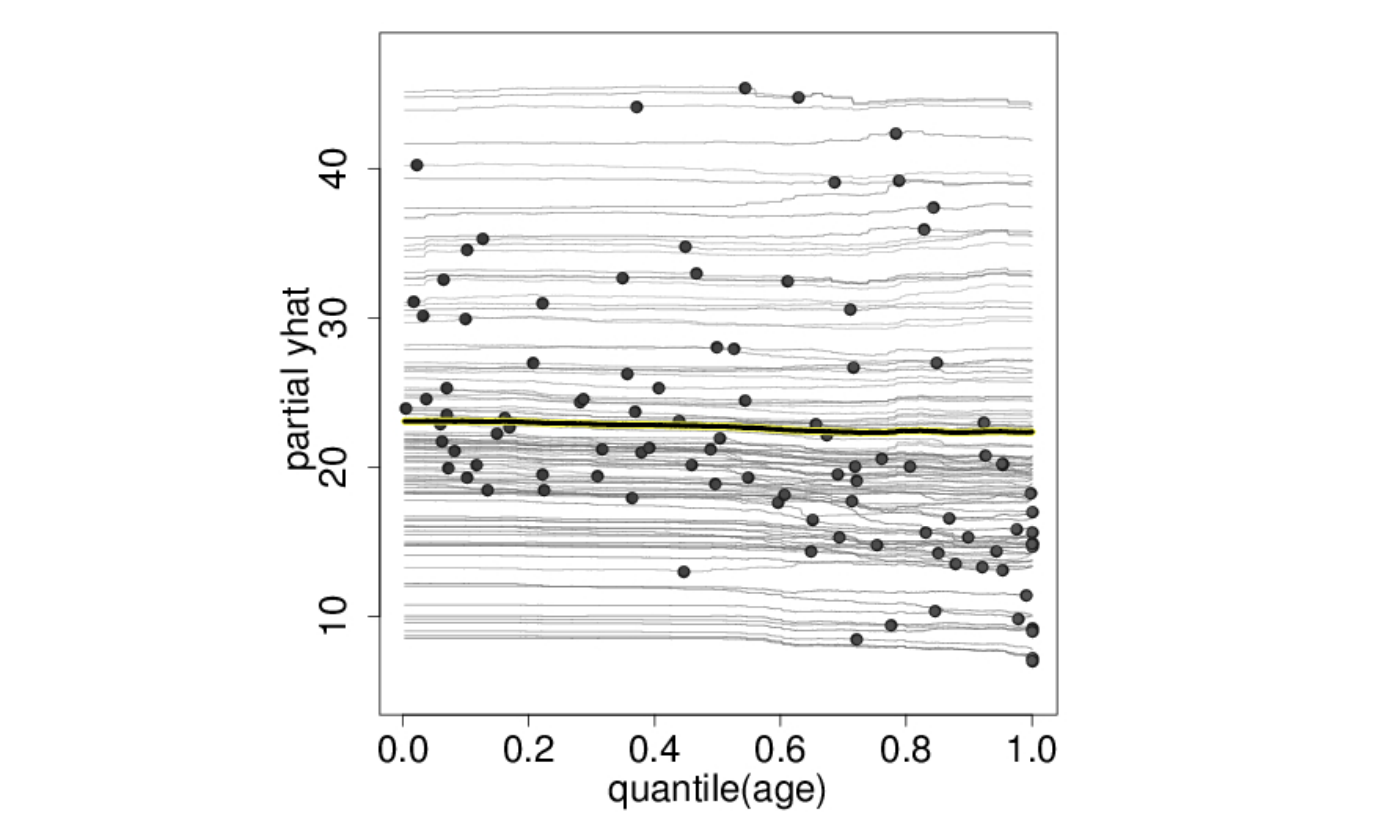
จากรูปด้านบน เราดูจากรูปแล้วสามารถบอกได้เลยรึเปล่าว่าฟีเจอร์ age ไม่มีผลต่อราคาบ้าน เพราะทุก ๆ เส้นมันก็ดูเรียบ ๆ เหมือนกันหมด คำตอบก็ต้องแน่นอนอยู่แล้วว่าไม่ได้จ้าาาาา ที่จริงแล้วน่ะ มันมีผล แค่อาจจะไม่ได้มีผลเยอะมากขนาดนั้น คือฟีเจอร์อื่น ๆ มันก็กำหนดราคาบ้านไว้ในแต่ระดับอยู่แล้ว แล้วฟีเจอร์นี้ก็อาจจะไปปรับเพิ่มลดนิดหน่อยเราก็เลยไม่เห็น (อย่าลืมว่าฟีเจอร์อื่น ๆ มีเป็นสิบตัว เช่น ทำเล, จำนวนชั้น, จำนวนห้องนอน ฯลฯ มันก็ต้องกำหนดระดับราคาบ้านได้มากกว่าฟีเจอร์อายุบ้านที่มีตัวเดียวอยู่แล้ว) 

เพราะฉะนั้นแล้ว เหล่าผู้คิดค้น ICE plot ก็เลยคิดว่า เราก็รวบค่า partial dependence ณ ตำแหน่งฟีเจอร์ที่เราสนใจที่น้อยที่สุดเข้าด้วยกันแล้วเอาไว้ที่ 0 ซึ่งคำนวณทางคณิตศาสตร์ด้วยสมการง่าย ๆ เลย

\begin{equation} \hat{f^{(i)}}_{cent} = \hat{f^{(i)}} - \pmb{1} \hat{f} ( x^{\ast} , \pmb{x}^i_C ) \end{equation}

เมื่อ 

• \(x\) คือ ฟีเจอร์ที่เราสนใจ
• \(x^\ast\) คือ ค่า min ของฟีเจอร์ที่เราสนใจ 
• \(\pmb{x}_C\) คือเซ็ตของฟีเจอร์อื่น ๆ ที่เราไม่ได้สนใจ
• \(\hat{f}(i) = \hat{f}(x_i,x_{Ci})\) หรือก็คือค่า partial dependence ที่เราพล็อตบนกราฟ ICE plot แบบธรรมดา
• \(\hat{f}(i)_{cent}\) คือค่า partial dependence ที่เราพล็อตบนกราฟ c-ICE

ถ้าใครยัง งง ๆ วิธีการทำ centered ICE plot ก็ไปดูรูปแรกเลยเด้อ มีวิธีพล็อตแบบ step-by-step ให้ดูอยู่จ้า

เพราะฉะนั้นแล้วจากรูป ICE plot ของ boston house dataset ด้านบนที่ดูยาก ๆ ไม่ค่อยเห็นอะไร ก็จะกลายเป็นรูป c-ICE plot ที่เห็นได้ชัดขึ้นว่าเมื่ออายุบ้านมากขึ้น บ้านบางหลังจะมีแนวโน้มราคาแพงขึ้น แต่บางหลังราคาถูกลง

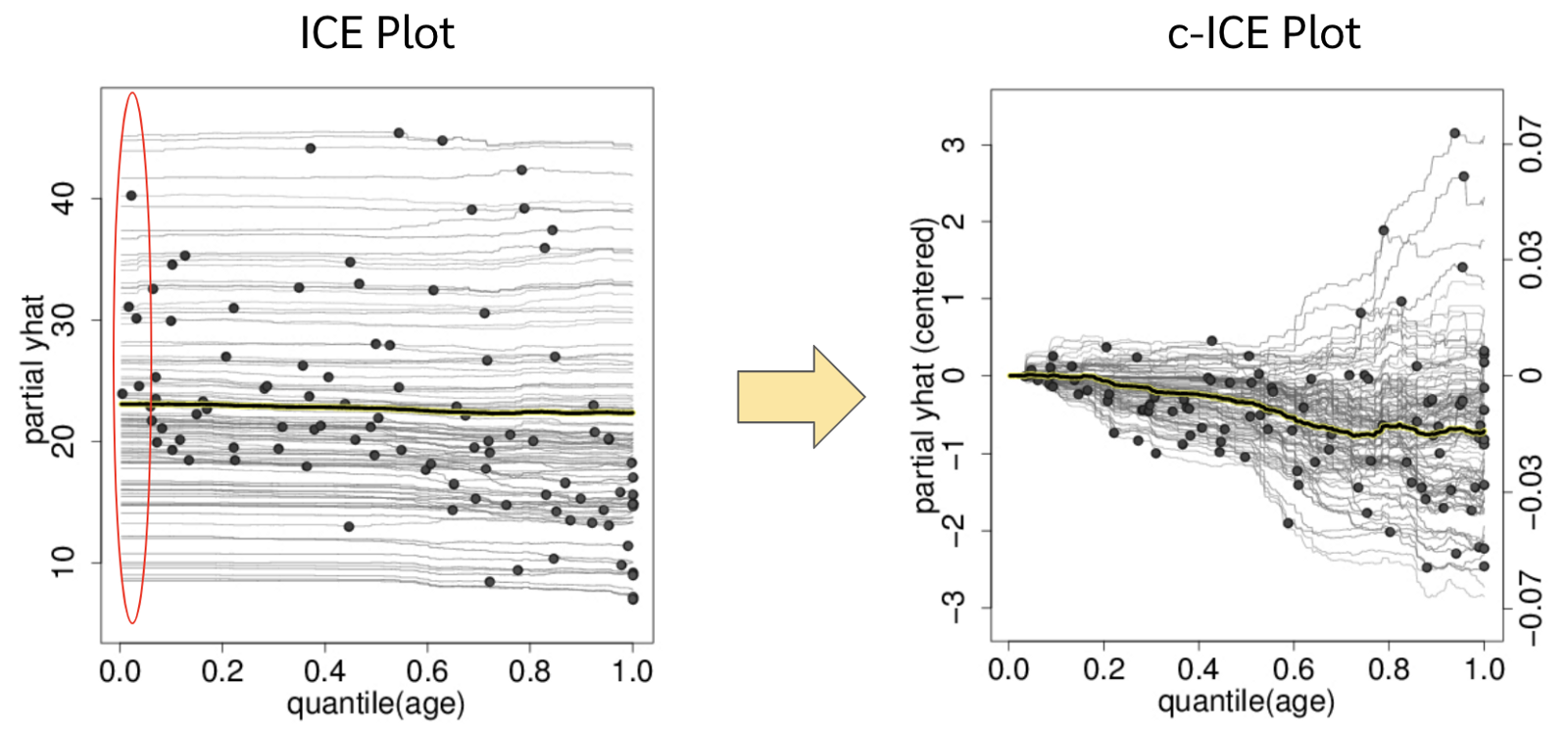
Coding

ในตัวอย่างนี้จะใช้ข้อมูล titanic dataset นะครับ ส่วนโค้ดทั้งหมดสามารถตาม link นี้ไปได้เลยครับ

1. ก่อนอื่น เราสร้างโมเดลสำหรับทำนายหรือ classify ขึ้นมาก่อน (ในบทความนี้จะขอผ่านส่วนของการ feature importance ไปนะครับ)

    ## Import lib ที่ใช้
    import numpy as np
    import pandas as pd
    import matplotlib.pyplot as plt
   
    ## อ่านข้อมูล และลบฟีเจอร์ที่ไม่ใช้ออก (ฟีเจอร์ Name)
    df = pd.read_csv('titanic.csv')
    df = df.drop(['Cabin','Name','Ticket','PassengerId'],axis=1).dropna()
   
    ## แบ่ง dataframe สำหรับฟีเจอร์ และ label
    features =  pd.get_dummies(df.drop('Survived',axis=1))
    labels = df['Survived']
   
    ## แบ่ง data สำหรับ train กับ test
    from sklearn.model_selection import train_test_split
    train_features,\
    test_features,\
    train_labels,\
    test_labels = train_test_split(features,\
                                    labels,\
                                    test_size = 0.25)
   
    # เทรนโมเดล
    from sklearn.ensemble import RandomForestClassifier
    rf = RandomForestClassifier(n_estimators=1000, max_depth=5)
    rf.fit(train_features, train_labels)
   

2. ในส่วนของ ice plot ด้วย python นั้น ขั้นแรกเราต้องลง library ที่ชื่อว่า pycebox ก่อน ซึ่งถูกพัฒนาโดยคุณ Austin Rochford แต่ในบทความนี้ ผม fork github เค้ามาแล้วมาแก้นิดหน่อย (แก้บั๊คบน python3 แล้วทำให้พล็อต color bar กับสร้าง legend ได้ง่ายขึ้น) ผู้อ่านสามารถก๊อบโค้ดจาก link นี้ไปวางในโค้ดได้เลยครับ

3. Import package ที่ใช้

    import pandas as pd
    import numpy as np
    import matplotlib.pyplot as plt
    import seaborn as sns
   

4. อ่านข้อมูลมาสร้างโมเดล

    ## อ่านข้อมูล และลบฟีเจอร์ที่ไม่ใช้ออก (ฟีเจอร์ Name)
    df = pd.read_csv('titanic.csv')
    df = df.drop(['Cabin','Name','Ticket','PassengerId'],axis=1).dropna()
    # del df['Name']
   
    ## แบ่ง dataframe สำหรับฟีเจอร์ และ label
    features =  pd.get_dummies(df.drop('Survived',axis=1))
    labels = df['Survived']
   
    ## แบ่ง data สำหรับ train กับ test
    from sklearn.model_selection import train_test_split
    train_features,\
    test_features,\
    train_labels,\
    test_labels = train_test_split(features,\
                                    labels,\
                                    test_size = 0.25)
   
    # เทรนโมเดล
    from sklearn.ensemble import RandomForestClassifier
    rf = RandomForestClassifier(n_estimators=1000, max_depth=5)
    rf.fit(train_features, train_labels)
   

5. ก่อนจะสร้าง ICE plot เราต้องสร้าง ICE df ก่อน ด้วยการใช้ฟังก์ชัน ice ซึ่งจะรับพารามิเตอร์ดังนี้
   • Dataset
   • ฟีเจอร์ที่เราสนใจหรือ \(x_s\)
   • ฟังก์ชันที่ใช้ทำนาย
     • ถ้าเป็น regression ผลลัพธ์การทำนายเราออกมาเป็นตัวเลขอยู่แล้ว ก็ใช้ <model>.predict ได้เลย
     • ถ้าเป็น classification เราต้องเลือกว่าจะดู effect ของ \(x_s\) ต่อ probability ของ class ไหน เสร็จแล้วเราสร้างฟังก์ชันที่ดึง probability ของ class นั้นขึ้นมา อย่างเช่นในบทความนี้เราจะดู effect ของ \(x_s\) ต่อ probability ที่จะรอดจากเรือไททานิค เราก็ใช้โค้ด get_prob_survive = lambda x: rf.predict_proba(x)[:,1] ได้เลย จะเห็นได้ว่าเราดึงเฉพาะ column ที่ 1 ของตาราง probability มาเท่านั้น
   • num_grid_points เป็นจำนวน grid resolution (ถ้าไม่ทราบว่าคืออะไร สามารถอ่านได้ที่ขั้นตอนที่ 2 ของการสร้าง pdp plot)

   เพราะฉะนั้นเราสามารถสร้าง ICE plot ได้ด้วย code ด้านล่างนี้

    ##################
    ## Gen Ice DF
    ##################
    get_prob_survive = lambda x: rf.predict_proba(x)[:,1]
    ice_df = ice(train_features, 'Age', get_prob_survive, num_grid_points=20)
   

   ซึ่ง ice_df ที่ได้จะเป็น dataframe ที่มี

   • จำนวน row เท่ากับจำนวน num_grid_points
   • มีจำนวน column เท่ากับจำนวน unique value ของ set ของฟีเจอร์อื่น ๆ ที่เราไม่ได้สนใจ \(x_C\)

   ถ้างงให้ไปดูตารางในขั้นตอนที่ 4 ในรูปแรกของบทความนี้ หรือจะย้อนไปดูในขั้นตอนการสร้าง pdp plot ก็ได้ แต่มีการกลับด้านของตารางนิดหน่อย

   ซึ่งถ้าเราเอา ice_df ออกมาดูจะหน้าตาแบบนี้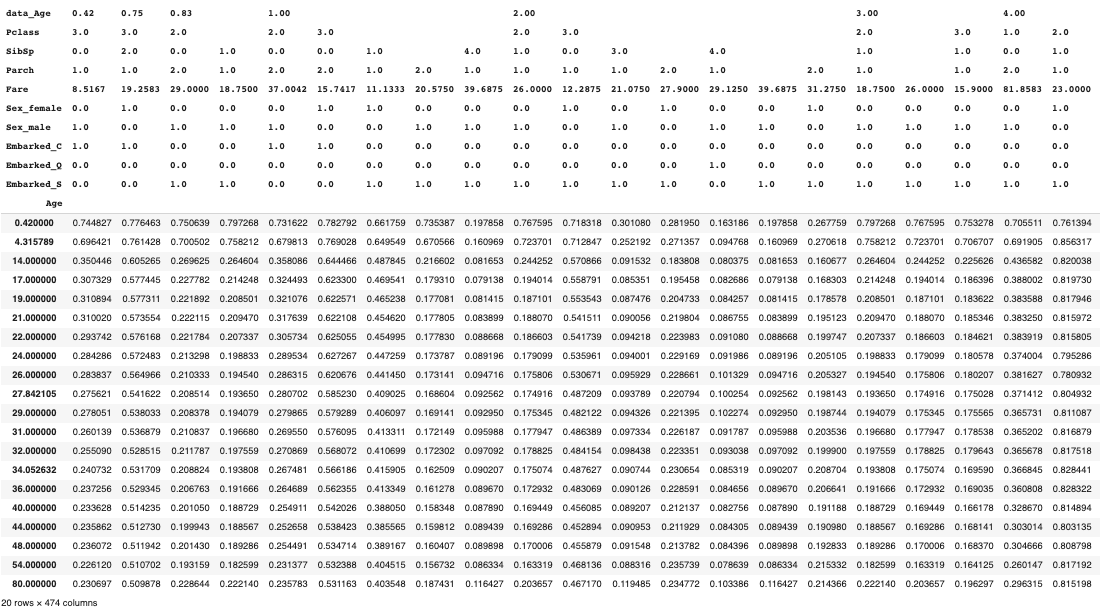

   

   จะเห็นได้ว่า

   • column นั้นจะมีหลาย level มาก ซึ่งแต่ละ level ก็คือแต่ละฟีเจอร์ในเซ็ต \(x_C\)
   • แต่ละ column คือ unique value ของ \(x_c\)
   • มีจำนวน rows เท่ากับจำนวน num_grid_points ที่เราใส่เข้าไป
   • ตัวเลขในตารางแต่ละช่องนั้นเกิดจาก การนำฟีเจอร์ \(x_s\) ณ ค่าของ row นั้น ไปประกอบกับฟีเจอร์ \(x_C\) ณ ค่าของ column นั้น แล้วนำไปเข้าฟังก์ชัน get_prob_survive

   ที่จริงแล้วการพล็อต ICE plot ก็คือการนำค่าในแต่ละ column ของ ice_df ไปพล็อตกราฟเส้นนั่นเอง

6. พล็อต c-ICE

    # กำหนดขนาดรูปและความละเอียด
    plt.figure(figsize=(10,5), dpi=130)
    # สร้าง ax ไว้พล็อต
    ax = plt.subplot(1, 1, 1)
    # พล็อต c-ICE
    ice_plot(ice_df,\
             frac_to_plot=0.2,
             alpha=0.25,
             ax=ax,\
             centered=True, \
             plot_pdp=True,\
             pdp_kwargs={'color':'red','linewidth':3})
   

   ซึ่งฟังก์ชัน ice_plot นั้นมีพารามิเตอร์ที่สำคัญ ๆ ดังนี้

   • ice_df ที่สร้างในข้อก่อนหน้า
   • frac_to_plot หรือก็คืออัตราส่วนของข้อมูลที่เราจะ sample มาพล็อต ต้องอย่าลืมว่า ice plot คือ pdp เวอร์ชั่นที่ไม่ได้เอาทุกเส้นมา average กัน เพราะฉะนั้นเวลาพล็อตออกมาจำนวนเส้นกราฟมันจะเยอะมาก ๆ (= จำนวนข้อมูลเรา) ถ้าพล็อตออกมาหมดมันจะรกไปหน่อย อยากพล็อตเท่าไหร่ก็ตั้งไปเท่านั้น อย่างในตัวอย่างด้านบนคือให้พล็อตประมาณ 20% จากจำนวนข้อมูลทั้งหมด
   • ax คือ object ของ matplotlib.axes._subplots.AxesSubplot เอาไว้พล็อตกราฟ
   • centered เอาไว้กำหนดว่าจะพล็อต ICE plot ธรรมดาหรือ c-ICE
     • ถ้าตั้งเป็น False คือพล็อต ICE plot ธรรมดา
     • ถ้าตั้งเป็น True คือพล็อต c-ICE
   • plot_pdp เอาไว้กำหนดว่าเราจะพล็อต PDP ออกมาด้วยรึเปล่า ซึ่งก็จะเกิดจากการเอาทุกเส้นไป average กันน่ะแหละ
   • pdp_kwargs เอาไว้กำหนดรูปแบบของเส้น PDP อย่างในตัวอย่างด้านบน เรากำหนดให้เป็นสีแดง และเส้นหนาขนาด 3 เพราะจได้ดูง่าย ๆ หน่อย

   ทีนี้เราก็จะได้ c-ICE มาแล้ว

   

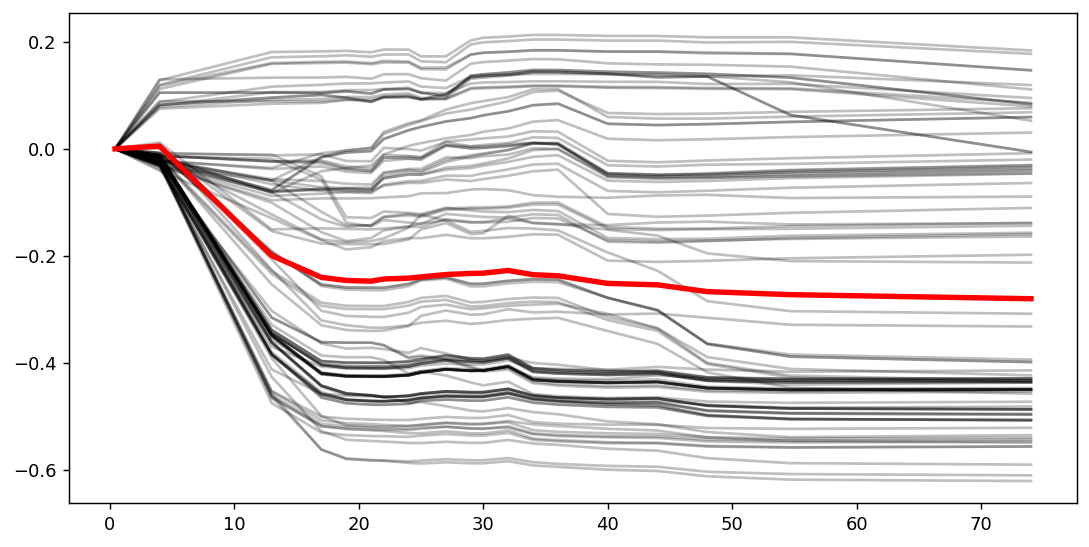
   แต่จะเห็นว่ามันจะยังโล่ง ๆ หน่อย เราก็เติมชื่อแกน x แกน y เข้าไปด้วยคำสั่ง

    ax.set_ylabel('Effect on Probaility of Surviving')
    ax.set_xlabel(focus_feature)
   

   ทีนี้ถ้าย้อนไปตอน PDP จะจำได้ว่า ตอนดูกราฟ PDP นั้นสิ่งสำคัญคือเราต้องดูจำนวนข้อมูลในแต่ละช่วงด้วย หรือก็คือดู Distribution ของฟีเจอร์ที่เราสนใจด้วย ซึ่งส่วนใหญ่มันจะแสดงในรูปแบบ rug plot แต่ตอนนี้มันยังไม่มี เราก็เติมได้ด้วยโค้ดด้านล่างนี้

    sns.distplot(train_features[focus_feature], ax=ax, hist=False, kde=False, rug=True, rug_kws={'color':'k'})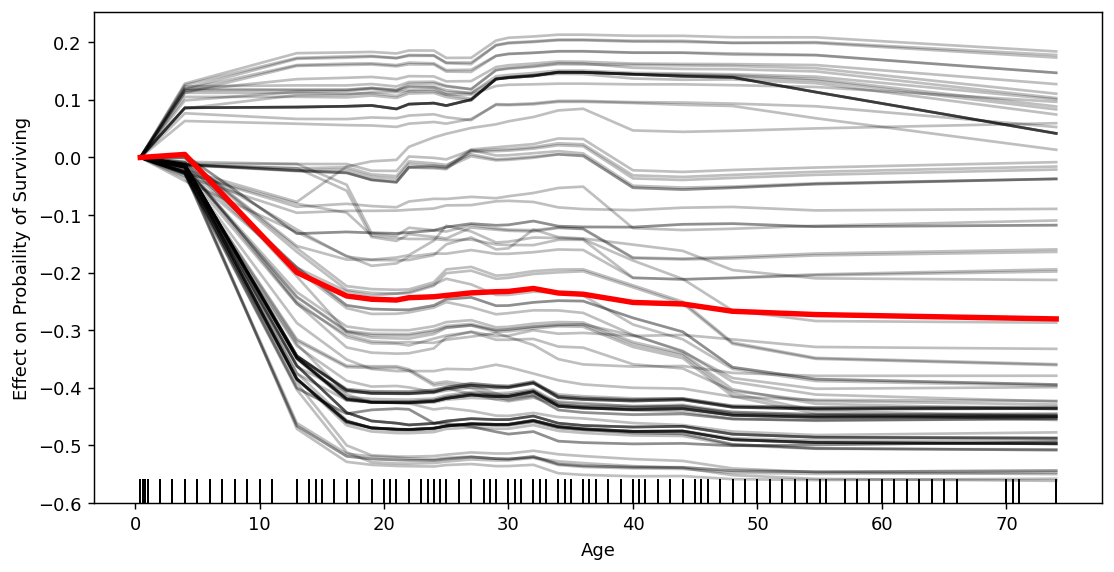
   

   

7. อย่างรูปด้านบน เราจะเห็นได้ว่าหากอายุมากขึ้นแล้ว บางกลุ่มมีโอกาสรอดชีวิตสูงขึ้น ในขณะที่บางกลุ่มมีโอกาสการรอดชีวิตน้อยลง ในขั้นตอนนี้หากเราจะทดลองดูแบบง่าย ๆ ว่ามีปัจจัยอื่น ๆ ที่สามารถแยกข้อมูลสองกลุ่มนี้ออกจากกันได้หรือไม่ เราสามารถนำฟีเจอร์หรือปัจจัยนั้น ๆ มาทำเป็นสีในพล็อตได้ ด้วยการเพิ่มพารามิเตอร์ color_by เข้าไปในคำสั่ง ice_plot อย่างเช่นในโค้ดด้านล่างนั้น เราจะใส่สีด้วยการดูจากฟีเจอร์ ‘Sex_female’ (0: เป็นผู้ชาย, 1: เป็นผู้หญิง)

    plt.figure(figsize=(10,5), dpi=130)
    ax = plt.subplot(1,1,1)
    ## Plot c-ICE
    ax,color_map = ice_plot(ice_df,\
                            frac_to_plot=0.2,\
                            alpha=0.25,
                            ax=ax,\
                            centered=True, \
                            plot_pdp=True,\
                            color_by='Sex_female',\
                            pdp_kwargs={'color':'red','linewidth':3})
   
    ## เพิ่มชื่อแกน x แกน y
    ax.set_ylabel('Effect on Probaility of Surviving')
    ax.set_xlabel(focus_feature)
   
    ## เพิ่ม Rug plot
    sns.distplot(train_features[focus_feature], ax=ax, hist=False, kde=False, 
                  rug=True, rug_kws={'color':'k'})
   
    ####################
    ## สร้าง legend หรือ color bar
    handles, labels = ax.get_legend_handles_labels()
    unique_label, unique_handle = [], []
    for handle, label in zip(handles, labels):
      if label not in unique_label:
        unique_label.append(label)
        unique_handle.append(handle)
    ax.legend(unique_handle, unique_label,title='Sex_female')
   

   จะได้รูปประมาณนี้ จะเห็นได้ว่าเมื่ออายุมากขึ้น ผู้หญิงนั้นมีแนวโน้มอัตราการรอดชีวิตสูงกว่าผู้ชาย ซึ่งจะเห็นได้ว่าในกลุ่มผู้หญิงนั้นเมื่ออายุเพิ่มขึ้น จะมีโอกาสรอดชีวิตเพิ่มขึ้นสูงสุดประมาณ +20% แต่ในกลุ่มผู้ชายนั้น เมื่ออายุสูงขึ้น จะมีโอกาสรอดชีวิตลดลงมากสุดประมาณ -60% ทีเดียว

   

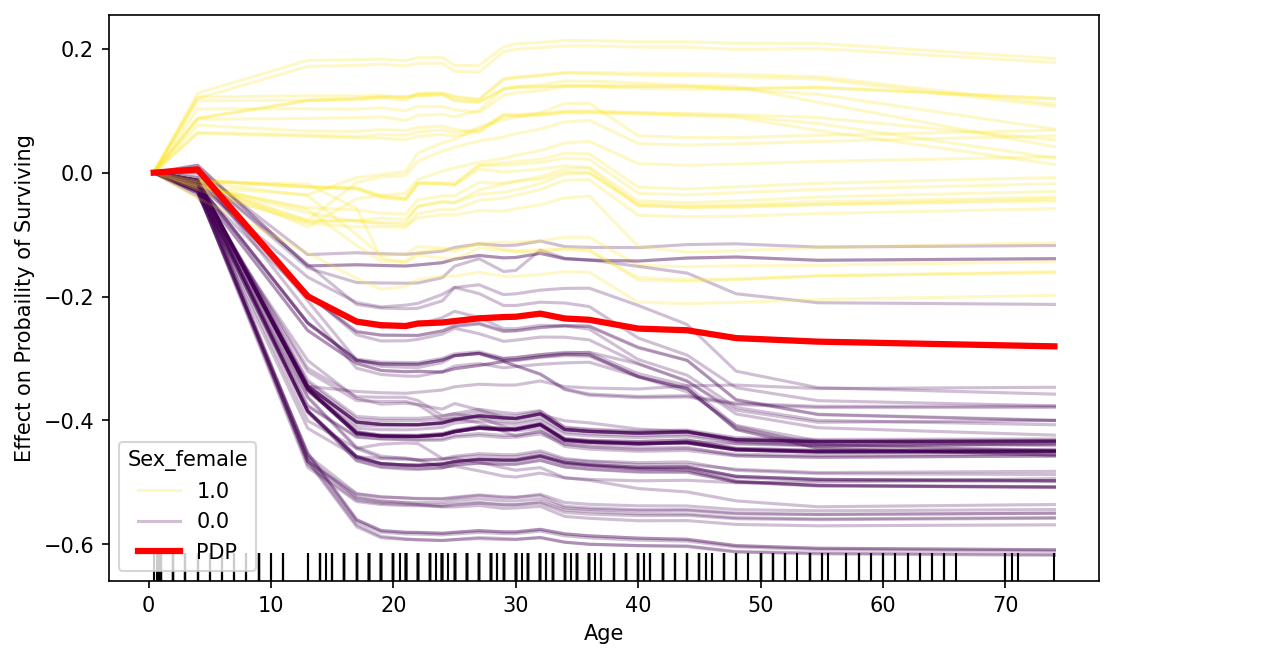
8. แต่ถ้าฟีเจอร์ที่เราจะเอามาใส่เป็นสีดันเป็นฟีเจอร์แบบตัวเลข เราต้องสร้าง color bar ไว้เพื่อดูเทียบด้วย ก็สามารถใช้โค้ดด้านล่างได้เลยครับ

    ## สร้าง subplot ขนาด 1 row, 2 columns เอาไว้พล็อต c-Ice และ colorbar
    fig, axs = plt.subplots(1,2,gridspec_kw={'width_ratios': [15, 1]}, figsize=(10,5), dpi=150)
   
    ## Plot c-ICE
    ax_plot,color_map = ice_plot(ice_df,\
                                  frac_to_plot=0.2,\
                                  alpha=0.25,
                                  ax=axs[0],\
                                  centered=True, \
                                  plot_pdp=True,\
                                  color_by='Fare',\
                                  pdp_kwargs={'color':'red','linewidth':3})
    ## ทำ color bar จาก color_map
    fig.colorbar(color_map,cax=axs[1], orientation='vertical', label='Fare')
   
    ## เพิ่มชื่อแกน x แกน y
    ax_plot.set_ylabel('Effect on Probaility of Surviving')
    ax_plot.set_xlabel(focus_feature)
   
    ## เพิ่ม Rug plot
    sns.distplot(train_features[focus_feature], ax=ax_plot, hist=False, kde=False, 
                  rug=True, rug_kws={'color':'k'})
   

   จะได้ประมาณนี้

   

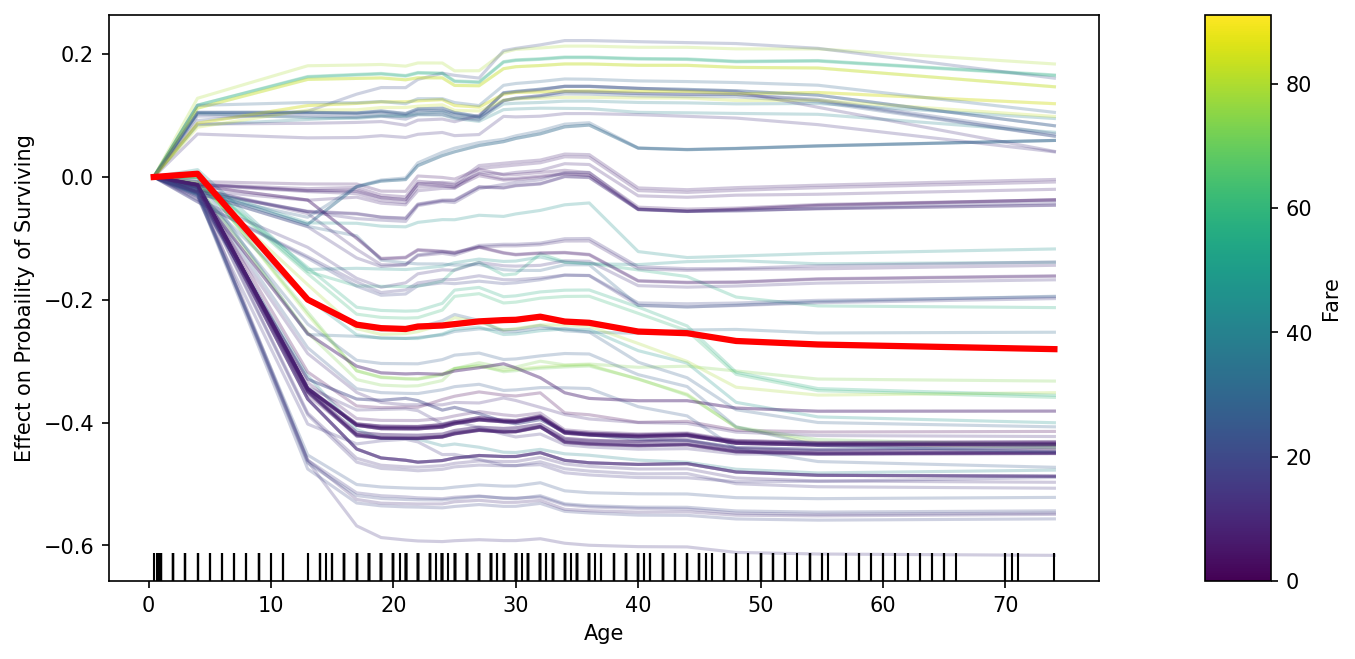
9. จากขั้นตอนทั้งหมด เราสามารถรวมๆได้โค้ดประมาณนี้ โดยที่เราอาจจะเช็คก่อนว่าค่า unique value เกิน 2 ค่ารึเปล่า (เปลี่ยนโค้ดได้ตามต้องการ) ถ้ามีแค่ 2 ค่าเราอาจจะทำเป็นแค่ legend แต่ถ้ามีมากกว่า 2 ค่าเราอาจจะทำเป็น color bar

    def c_ice_color_by(data, focus_feature,color_by):
      ## สร้าง ice_df
      ice_df = ice(data, focus_feature, get_prob_survive, num_grid_points=20)
   
      ## สร้าง ax ไว้พล็อต
      fig, axs = plt.subplots(1,2,gridspec_kw={'width_ratios': [15, 1]}, figsize=(10,5), dpi=150)
   	  
      ## พล็อต c-ICE
      ax_plot,color_map = ice_plot(ice_df,\
                                    frac_to_plot=0.2,\
                                    alpha=0.25,
                                    ax=axs[0],\
                                    centered=True, \
                                    plot_pdp=True,\
                                    color_by=color_by,\
                                    pdp_kwargs={'color':'red','linewidth':3})
   
   	  
      ####################
      ## สร้าง legend หรือ color bar
      handles, labels = ax_plot.get_legend_handles_labels()
      unique_label, unique_handle = [], []
      for handle, label in zip(handles, labels):
        if label not in unique_label:
          unique_label.append(label)
          unique_handle.append(handle)
      ## ถ้าจำนวน category มีไม่เกิน 2 ให้สร้าง legend (ตั้งไว้เป็น 2+1 ที่ <=+1 เพราะมี label ของ PDP ด้วย)
      if len(unique_label)<=3:
        ax_plot.legend(unique_handle, unique_label,title=color_by)
        ## ถ้าสร้างแค่ legend อีก ax นึงก็ไม่ต้องใช้ เราก็ปิดไป
        axs[1].axis('Off')
      ## แต่ถ้ามีมากกว่านั้นให้ทำ color bar
      else:
        fig.colorbar(color_map,cax=axs[1], orientation='vertical', label=color_by)
   
      ## เซ็คคำอธิบายแกน x และ y
      ax_plot.set_ylabel('Effect on Probaility of Surviving')
      ax_plot.set_xlabel(focus_feature)
   
      ## สร้าง rug plot
      sns.distplot(train_features[focus_feature], ax=ax_plot, hist=False, kde=False, 
                    rug=True, rug_kws={'color':'k'})
   

   ตัวอย่างการเรียกใช้

    c_ice_color_by(train_features,'Sex_female','Pclass')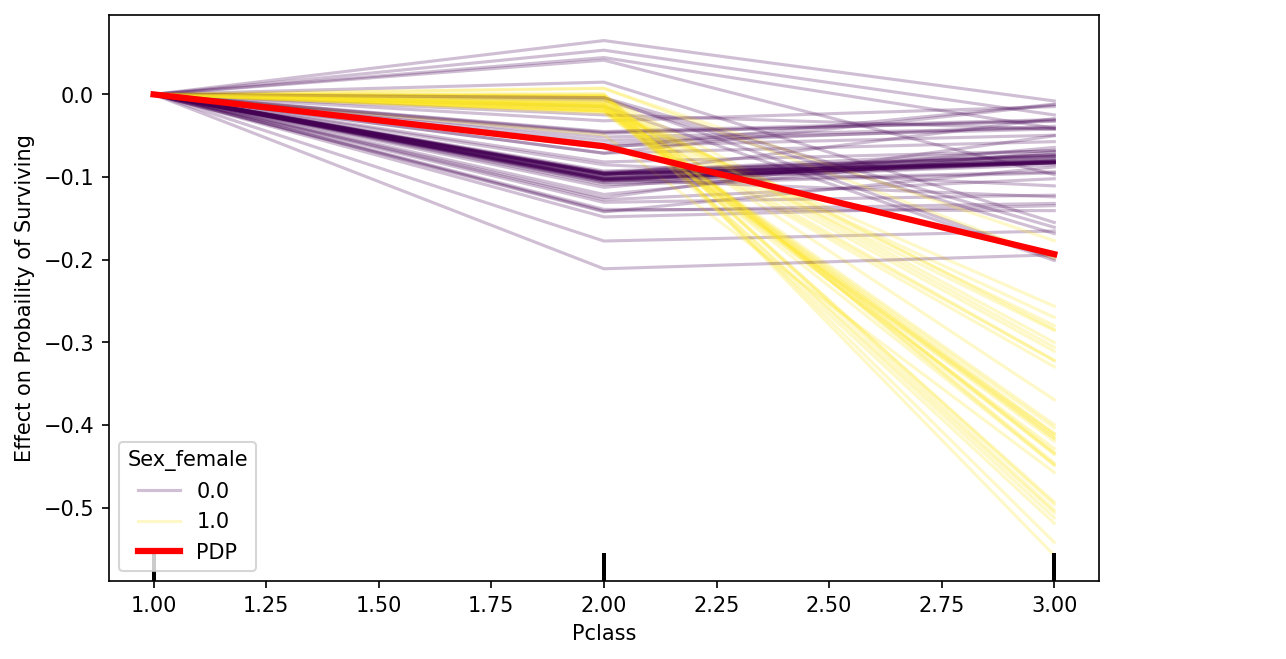
   

   

   ** หมายเหตุ: ฟีเจอร์ Pclass คือระดับชั้นของการเดินทาง 1 คือหรูสุดแพงสุด และระดับชั้นที่ 3 คือถูกที่สุด

   ซึ่งจะเห็นได้ว่่า กลุ่มผู้ชาย(เส้นสีม่วง)นั้นส่วนใหญ่ มีอัตราการรอดชีวิตพอๆกันในทุกๆ class แต่ในกลุ่มผู้หญิง(สีเหลือง)นั้นเมื่อ class เป็น 3 นั้นจะมีอัตราการรอดชีวิตลดลงโดยเฉลี่ยประมาณ 20% - 50% เลยทีเดียว ซึ่งแปลความได้ว่าค่า Pclass นั้นจะมีผลเฉพาะกลุ่มข้อมูลที่เป็นผู้หญิง

Ref.

[1] Peeking Inside the Black Box: Visualizing Statistical Learning with Plots of Individual Conditional Expectation https://arxiv.org/pdf/1309.6392.pdf