ในบทความนี้จะ intro วิธีของ reinforcement learning ในฝั่งของ policy-based reinforcement learning กันบ้าง หลังจากพอจะรู้จักกับ Q-learning, Deep Q Learning ที่เป็น value-based reinforcement learning กันมาแล้ว ซึ่งวิธีที่จะนำมาเขียนในบทความนี้ค่อนข้างจะเก่ามาก (น่าจะประมาณ 20 ปีได้) แล้วก็อาจจะไม่มีใครใช้กันแล้วในปัจจุบัน แต่ก็เป็นประตูที่ดีสู่ความเข้าใจในวิธีอื่น ๆ ในปัจจุบัน เพราะฉะนั้นแล้ว อ่านเถอะ
Prerequisite Knowledge
ก่อนจะเข้าเรื่อง Policy Gradient อยากเท้าความถึงความรู้ที่เราควรรู้ก่อนเริ่มกันก่อน
Markov Decision Process
ใน Markov Decision Process นั้นเป็น extension ของ markov chain โดยการเพิ่มส่วนของ action และ reward เข้าไป ซึ่งองค์ประกอบหลัก ๆ ของ MDP นั้นได้แก่
- State ($S$) หรือสถานการณ์ใด ๆ ที่เป็นไปได้ทั้งหมด ยกตัวอย่าง เช่น ถ้าเป็นเกม state ก็คือหน้าจอของเกม
- Action ($A$) หรือการกระทำที่เราสามารถเลือกทำได้ เช่น ถ้าเป็นเกม action ก็เป็นปุ่มกดบนจอย
- State transition probability ($P(s’|s,a)$) หรือความน่าจะเป็นของการเปลี่ยนจาก state $s$ ไปยัง $s’$ โดยที่กระทำ action $a$
- Reward function ($R(s,a)$) หรือก็คือรางวัลที่จะได้รับหลังจากการทำ action $a$ ใน state $s$
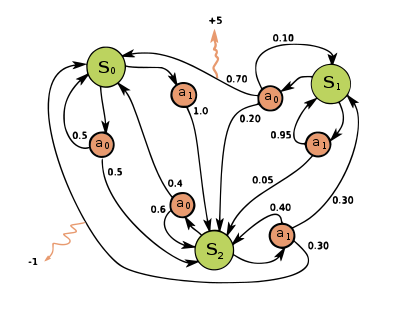
ซึ่งเมื่อเราโมเดลปัญหาเป็น MDP แล้วนั้น ปัญหาที่เราต้องการจะแก้จะเป็นการพยายาม optimize ค่า cumulative reward หรือ reward สะสมในระยะยาวดังแสดงในสมการที่ \eqref{eq:Gt} โดยที่ $\gamma$ เป็นค่าระหว่าง 0-1 เอาไว้กำหนดความสำคัญของ reward ในอนาคต
\begin{equation} \label{eq:Gt} G_t = \sum_{t=1}^{\infty} \gamma^t r_t \end{equation}
ซึ่ง reinforcement learning ก็เป็นวิธีแก้ปัญหา MDP ด้วยการออกแบบ policy function หรือ $\pi$ ซึ่งเป็น function ที่สามารถตัดสินใจได้ว่าควรทำ action ใดในแต่ละ state เพื่อให้ได้รับ cumulative reward มากที่สุด
\begin{equation} \label{eq:basic-policy} a^\ast = \pi(s) \end{equation}
ซึ่งสิ่งที่ทำให้การแก้ MDP มันยากก็คือ เรามักจะไม่รู้ว่า MDP ของปัญหาที่เรากำลังฝึก agent อยู่นั้นเป็นอย่างไร หรือก็คือไม่รู้ค่า $P(s’|s,a)$ และค่า $R(s,a)$ นั่นเอง ซึ่งก็หมายความว่าเราต้องลองผิดลองถูกและเก็บประสบการณ์มาพัฒนาการตัดสินใจของ policy function เอาเอง
ก็คือให้มอง environment เป็น black box ไป ที่เราใส่ action เข้าไป แล้วจะได้ reward และ state ถัดไปออกมาเพื่อพิจารณา action ถัดไปอีกที แต่เราไม่รู้กระบวนการทำงานของ black box นั้น โดยที่เราก็จะมอง reward เป็นเหมือน feedback ว่าการทำ action นั้นใน state นั้นดีหรือไม่ดีขนาดไหนและนำไปพัฒนาระบบการตัดสินใจอีกที
Stochastic Policy
ในบทความที่ผ่านมาทั้ง Q learning และ Deep Q Learning นั้น เราจะใช้ policy แบบง่าย ๆ คือเลือก action ที่มีค่า $Q$ มากที่สุด หรือก็คือ $a^\ast = \pi(s) = argmax_a Q(s,a)$ นั่นเอง ซึ่งเราจะเรียก policy นี้ว่า deterministic policy เพราะว่าถ้าเรารู้ค่า $Q$ เราก็รู้ action ที่แน่นอนอยู่แล้ว
แต่ใน Policy Gradient เนี่ย เค้าจะใช้ stochastic policy กัน ซึ่งคำว่า stochastic มันก็แปลว่าสุ่ม ก็แปลตรงตัวได้เลยว่าตัว stochastic policy คือ policy แบบที่สุ่ม action เอา พูดได้อีกอย่างนึงก็คือถ้าเราใส่ state เดิมเข้าไปใน policy ก็อาจจะไม่ได้ action เดิมก็ได้
แล้วถ้าเราสุ่มเลือก action แล้ว agent เราจะทำงานได้ดีได้ยังไง ?
ใน stochastic policy นั้น ถึงเราบอกว่าเราสุ่ม action มา แต่เราก็ไม่ได้สุ่มทุก action ด้วย probability เท่ากันหมด โดยที่ probability ในการหยิบ action นั้นจะเป็น conditional probability หรือเขียนแบบคณิตศาสตร์ได้เป็น $P(a | s)$ แต่ว่าใน reinforcement learning เราจะเขียนให้คูล ๆ กว่าเดิมด้วยการเขียนเป็น $\pi(a|s)$ ซึ่งเราจะเรียกมันว่า policy น่ะแหละ
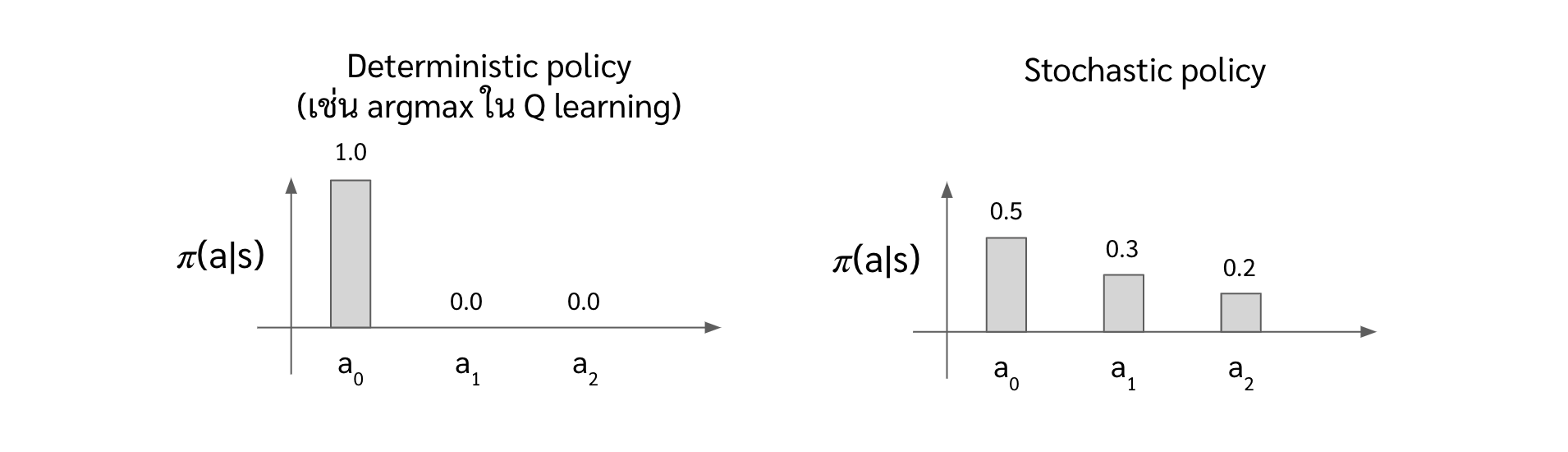
โดยที่การประมาณค่า $\pi(a|s)$ ที่เหมาะสมนั่นก็คือหน้าที่ของ policy gradient algorithm นั่นเอง
Policy Gradient
ในส่วนนี้จะพาทุกคนไปทำความรู้จักกับ policy gradient algorithm ว่ามันเป็นอย่างไร และเราจะสามารถเทรนมันได้อย่างไร
Overview of Policy Gradient
สำหรับตัว policy gradient นั้น เราจะใช้ neural network ในการประมาณค่า stochastic policy ของแต่ละ state ที่ใส่เข้าไปให้เราโดยตรง จากรูปด้านล่างจะเห็นว่า output แต่ละ node ของ neural network นั้นจะเป็น probability ของการเลือกแต่ละ action
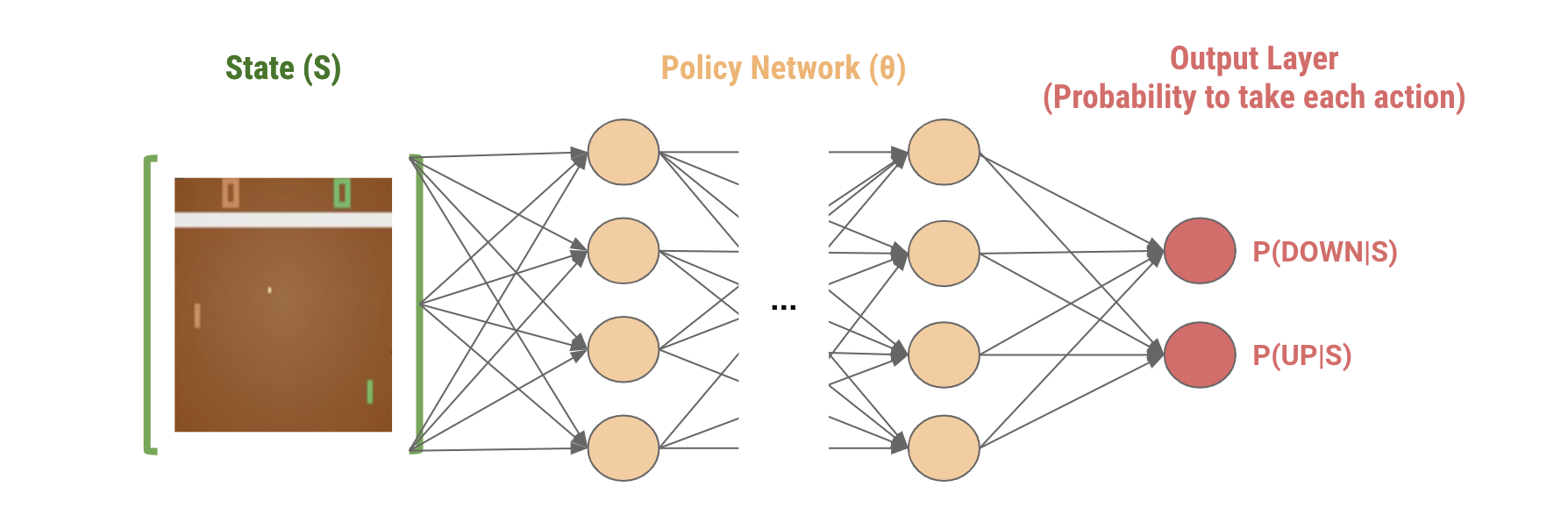
ซึ่งสิ่งที่ policy gradient ทำก็คือพยายามปรับค่า neural network parameter เพื่อให้สามารถประมาณค่า $P(action|state)$ ที่ทำให้ได้ reward ในระยะยาวหรือค่าในสมการที่ \eqref{eq:Gt} มากที่สุด หรือก็คือพยายามทำให้ neural network ประมาณค่า policy ที่ดีที่สุดให้ได้นั่นเอง
จะเห็นได้ว่าตัว Policy Gradient นั้น เราใช้ตัว stochastic policy เป็นหลัก เนื่องจากว่ามันทำให้เราค่อย ๆ optimize ค่า objective function ได้แบบ smooth มากขึ้น ซึ่งจะเหมาะกับการทำ gradient ascent มากกว่า
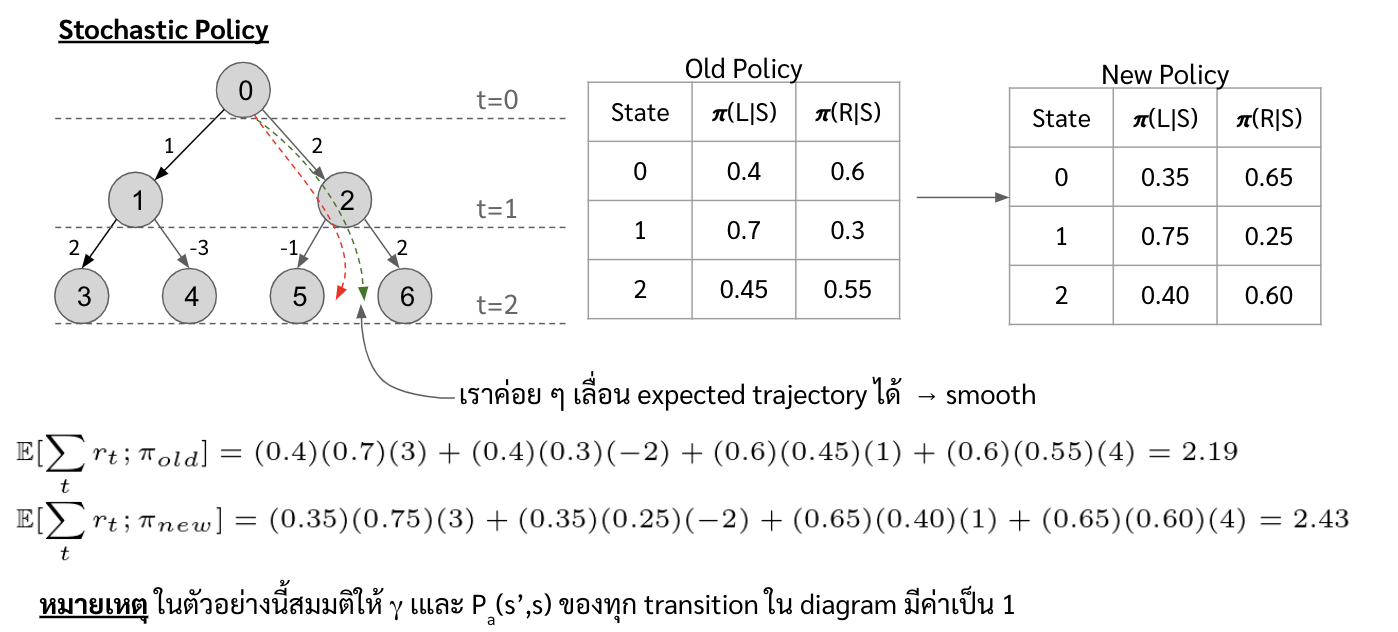
ซึ่ง gradient ascent นั้นก็จะอยู่ในรูปของสมการด้านล่าง ซึ่งก็คือเราพยายามหาความทิศทางของค่า $G_t$ เมื่อเทียบกับค่า $\theta$ แล้วค่อย ๆ ปรับ $\theta$ ไปในทิศทางที่ทำให้ค่า $G_t$ เพิ่มขึ้น
\begin{equation} \label{gradient-ascent-basic} \theta = \theta + \alpha \nabla_\theta G_t \end{equation}
โดยที่ตัว gradient ของ $G_t$ หรือ $\nabla_\theta G_t$ ในสมการด้านบน เค้าก็คิดมาให้แล้วว่ามันจะมีหน้าตาแบบนี้
\begin{equation} \label{overview} \frac{1}{m} \sum_{i=1}^{m} \sum_{t=0}^{H} \Bigg{(} {\color{blue} \nabla_\theta log\pi(a_t^{(i)}|s_t^{(i)})} {\color{green} \Big{(}\sum_{ t’=t}^{H} r(s_{t’}^{(i)},a_{t’}^{(i)})\Big{)}}\Bigg{)} \end{equation}
โดยที่
- $m$ คือจำนวน trajectory
trajectory ก็คือ serie ของประสบการณ์ที่ได้จากการทดลองใช้ agent ไป interact กับ environment ซึ่งจะประกอบไปด้วย state, action, และ reward ต่อกันไปเรื่อย ๆ
- $H$ คือความยาวของแต่ละ trajectory
- $s_t^{(i)}$ คือ state ณ เวลา $t$ ใน trajectory ที่ $i$
- $a_t^{(i)}$ คือ action ณ เวลา $t$ ใน trajectory ที่ $i$
- $r_t^{(i)}$ คือ reward ณ เวลา $t$ ใน trajectory ที่ $i$
ซึ่งถ้าเรามองแบบง่าย ๆ เลยจะเห็นได้ว่า เราพยายามจะปรับ probability ของ action นั้น ตามทิศทางและน้ำหนักของ summation ของ reward หลังจาก action นั้น หรือพูดอีกอย่างก็คือเรา weight ตัว gradient ของแต่ละ action ด้วย summation ของ reward หลังจากนั้นนั่นเอง
ซึ่งเดี๋ยวในหัวข้อถัดไปเราจะมาดูกันว่าสมการ \eqref{overview} มันมาได้ยังไง ซึ่งก็อาจจะยาวหน่อย แต่ก็อ่านเถอะนะ
Policy Gradient in Detail
ถ้าเรามองย้อนกลับไปในสมการที่ \eqref{eq:Gt} นั้นจะเห็นได้ว่าตัว objective function นั้นเป็น summation ของ rewards ในระยะยาว หรือ $\sum_{t=1}^{\infty} \gamma^t r_t$
แต่เดี๋ยวหลังจากนี้เราจะละ $\gamma$ ออกไปก่อน เพื่อความเข้าใจง่าย
แต่ว่าถ้านึกย้อนกลับไปยัง MDP และ Stochastic Policy นั้นจะเห็นได้ว่าตัว serie ของ reward ที่เราจะนำมา sum นั้นมันมีได้หลายแบบมาก เนื่องจากว่า $P(s’|s,a)$ ซึ่งอาจจะมีค่ากระจาย ๆ กันไป เช่นในด้านล่าง ถ้าเราอยู่ใน state $S_1$ แล้วเราเลือก action $a_0$ นั้น มีโอกาสที่จะเกิดเหตุการณ์ได้ 3 แบบด้วยกัน
- ขยับไป state $S_0$ และได้ reward +2
- กลับมา state $S_1$ และได้ reward 0
- ขยับไป state $S_2$ และได้ reward 0

นอกจากนี้ ถ้าเราใช้ stochastic policy ซึ่งใน state เดียวกัน เราอาจจะสุ่ม action ได้คนละแบบก็ได้ ซึ่งถ้าได้ action คนละแบบก็จะทำให้ได้ค่า $P(s’|s,a)$ ที่แตกต่างกันซึ่งอาจจะนำไปประสบการณ์ที่แตกต่างกันและได้รับ reward แตกต่างกันไปด้วย
สรุปก็คือในแต่ละรอบที่เราให้ agent ไป interact กับ environment นั้น รูปแบบของประสบการณ์ที่ได้จะเป็นไปได้หลายแบบมาก ๆ เนื่องจากมีการสุ่มทั้ง state และ action ในแต่ละ timestep
ซึ่งเราจะเรียก serie ของประสบการณ์ที่แตกต่างกันนั้นว่า trajectory หรือแทนว่า $\tau$ ซึ่งมันจะมีหน้าตาดังด้านล่าง ซึ่งจะเห็นได้ว่ามันประกอบไปด้วย state,action,reward ไปเรื่อย ๆ
\begin{equation} \label{tau} \tau = {s_1,a_1,r_1,s_2,a_2,r_2,…,s_H,a_H,r_H} \end{equation}
งั้นก็แปลว่าเราต้องเขียน objective function ให้เป็นค่าเฉลี่ยของผลรวมของ reward จากทุก $\tau$ ดังแสดงในสมการด้านล่าง เมื่อ $N$ คือจำนวน trajectory ทั้งหมดที่เป็นไปได้
\begin{equation} \label{average-from-tau} \mathbb{E}[\sum_{t=1}^{\infty} r_t] = \frac{\sum_{\tau} \sum_{t=1}^{\infty} r^\tau_t}{N} \end{equation}
แต่ว่าแต่ละ $\tau$ นั้นอาจจะมีโอกาสเกิดขึ้นเยอะหรือเกิดขึ้นน้อยแตกต่างกันไป เราก็เลยจะ weight มันด้วย probability ของ $\tau$ นั้น
\begin{equation} \label{weight-average-from-tau} \mathbb{E}[\sum_{t=1}^{\infty} r_t] = \sum_{\tau} P(\tau;\theta) R(\tau) \end{equation}
โดยที่
-
$P(\tau; \theta)$ คือ probability ของ trajectory $\tau$ เมื่อเราใช้ policy ที่มาจาก neural network parameter $\theta$ ซึ่งก็คือเราสามารถกระจายมันออกมาได้ในรูปดังนี้
\begin{equation} \label{p-tau} P(\tau;\theta) = {\color{purple}P(s_0)} \prod_{t=0}^{\color{blue}H} {\color{brown} P(s_{t+1}|s_t,a_t)} {\color{green} \pi_\theta(a_t|s_t)} \end{equation}
\[{\color{purple}s_0},{\color{green}a_0},r_0,{\color{brown}s_1},{\color{green}a_1},r_1,...,{\color{brown}s}_{\color{blue}H},{\color{green}a}_{\color{blue}H},r_{\color{blue}H}\]จะเห็นได้ว่า
- เราจะเริ่มจากการหา probability ของ state $s_0$ ก่อน (ซึ่งก็คือสมมติว่าเราจะสุ่มเกิดใน state ไหนก็ได้ ณ เวลา $t=0$ โดยที่ state $s_0$ ที่อยู่ใน trajectory นั้น มีโอกาสการเกิดเป็น $P(s_0)$)
- หลังจากนั้นเราก็จะไปดูว่า ณ state $s_0$ นั้นมี probability ในการเลือก action $a_0$ ที่อยู่ใน trajectory เป็นเท่าไหร่ หรือก็คือค่า $\pi_\theta (a_0|s_0)$
- และเราก็จะมาดูต่อว่าถ้าเราเลือก action $a_0$ ใน state $s_0$ แล้ว ค่า probabiltiy ที่ state ถัดไปจะเป็น $s_1$ เป็นเท่าไหร่ หรือก็คือค่า $P(s_1|s_0,a_0)$
แล้วเราก็นำทั้ง 3 ค่าด้านบนมาคูณกัน หลังจากนั้นเราก็คูณกับ $\color{green}\pi_\theta(a_1|s_1)$ กับ $\color{brown}P(s_2|s_1,a_1)$ และคูณค่าทั้งสองนี้ของ state และ action ถัดไปต่อไปเรื่อย ๆ จนครบทั้ง trajectory เราก็จะได้ค่า probability ของ trajectory นั้นแล้ว
ท่องไว้ว่า probability ของเหตุการณ์ที่เกิดต่อกันเราจะนำมาคูณกัน
Note อย่าสับสน notation ของ time ใน state, action, และ reward นะ เช่น
- $s_0$ คือ state ณ เวลา 0 ซึ่งอาจจะเป็น state อะไรก็ได้ เช่น A B C ขึ้นอยู่กับ $P(s)$ ณ เวลา 0 เช่น $P(A)$, $P(B)$, $P(C)$ อาจจะมีค่าเป็น 0.5,0.2,0.3
- $a_0$ คือ action ที่เราทำไป ณ เวลา 0 ก็อาจจะเป็น action อะไรก็ได้ เช่น < หรือ > ขึ้นอยู่กับ $\pi(s|a)$ เช่น $\pi(A|<)$, $\pi(A|>)$ อาจจะมีค่าเป็น 0.2 และ 0.8 ซึ่ง trajectory ที่เป็นไปได้อาจจะออกมาในหน้าตา
\[\tau = A,>,10,B,<,5,B,>,100,C,<,-10,A,<,10\]
ซึ่งก็คือ $s_0$ เป็น A และ $a_0$ เป็น > และ $r_0$ เป็น 10 นั่นเอง และค่า $P(s_1|s_0,a_0)$ ก็คือค่า $P(B|A,>)$ นั่นเอง
-
$R(\tau)$ คือ reward โดยรวมของ trajectory นั้น หรือก็คือ summation ของ reward ใน trajectory นั้นนั่นเอง
\begin{equation} \label{r-tau} R(\tau) = \sum_{t=0}^{\color{blue}H} {\color{green} r_t} \end{equation}
\[s_0,a_0,{\color{green}r_0},s_1,a_1,{\color{green}r_1},...,s_{\color{blue}H},a_{\color{blue}H},{\color{green}r_{\color{blue}H}}\]
ตอนนี้เราก็ได้ทำความรู้จักกับสมการเป้าหมายที่เราจะ maximize ค่ามาแล้วซึ่งก็คือสมการที่ \eqref{weight-average-from-tau} และอย่างที่เราบอกไปว่า policy gradient นั้นเป็นวิธีในการปรับค่า neural network parameter หรือ $\theta$ ที่จะทำให้ตัว neural network นั้นสามารถประมาณ policy function ที่ดีที่สุดได้ หรือก็คือเราสามารถเขียนเป้าหมายของ policy gradient ได้ในรูปแบบด้านล่าง
\begin{equation} \label{objective-2} \theta^\ast = argmax_\theta \sum_{\tau} P(\tau;\theta) R(\tau) \end{equation}
โดยที่วิธีที่เราจะนำมาใช้ก็คือ gradient ascent นั่นเอง ก็คือเราจะหา ค่า gradient ของ $\sum_{\tau} P(\tau;\theta) R(\tau)$ ต่อค่า $\theta$ และ ค่อย ๆ ปรับค่า $\theta$ จนได้ค่า $\sum_{\tau} P(\tau;\theta) R(\tau)$ มากที่สุด
\begin{equation} \label{gradient-ascent} {\color{green}\theta = \theta + \alpha} {\color{brown}\nabla_\theta \sum_{\tau} P(\tau; \theta) R(\tau)} \end{equation}
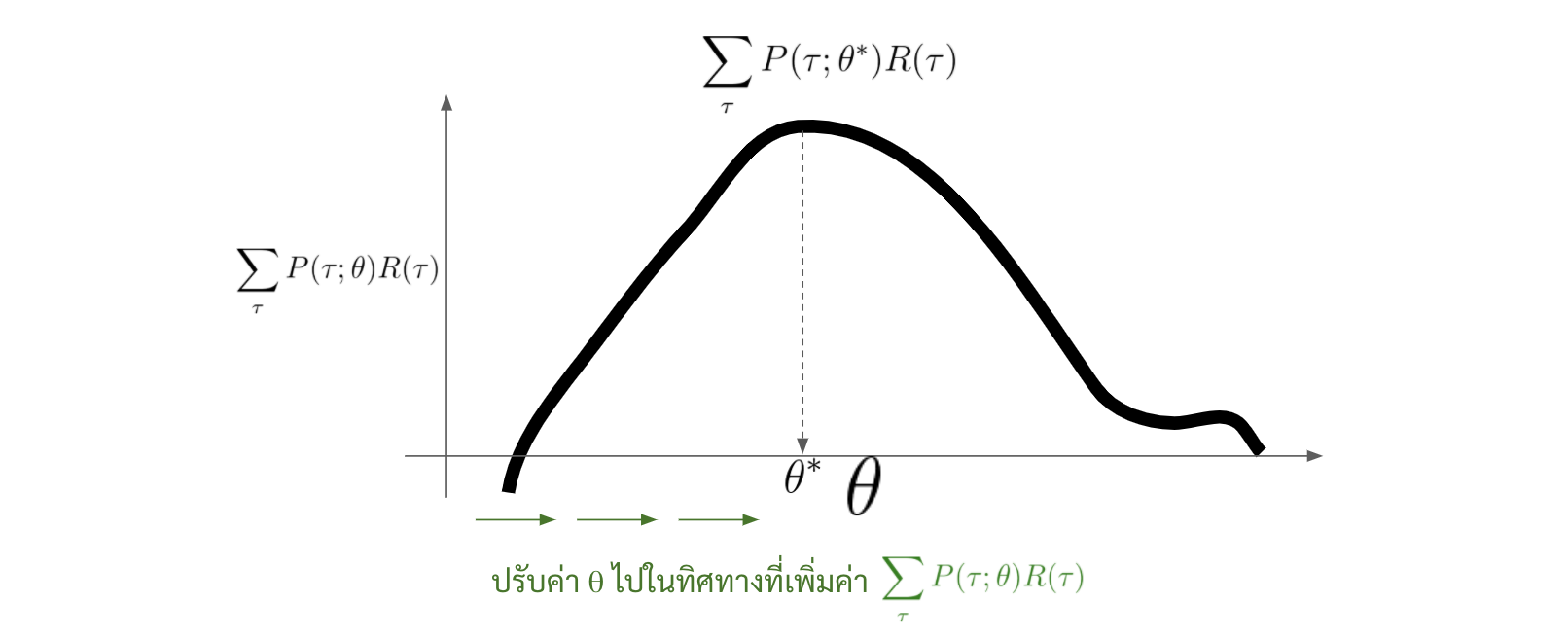
แต่ว่าการหาค่า $\nabla_\theta \sum_{\tau} P(\tau; \theta) R(\tau)$ นั้น ตอนนี้มันยังติดปัญหาสำคัญอยู่สองประการด้วยกัน
- จะเห็นได้ว่าตัว objective function ของเรามันเป็น summation ของทุก $\tau$ ซึ่งจำนวน $\tau$ ที่เป็นไปได้อาจจะมีเยอะมาก ซึ่งการสร้าง $\tau$ แต่ละครั้งเราจะปล่อยให้ agent เราได้ไปเล่นใน environment จนจบ episode หนึ่ง ซึ่งใน environment ที่มีความ complex หน่อย ๆ การปล่อยให้ agent เล่นใน environment จนได้ครบทุก $\tau$ ที่เป็นไปได้นั้นอาจจะเป็นไปไม่ได้เลย เพราะมันอาจจะต้องเล่นเป็นจำนวนหลายรอบมาก ๆ
ตัวอย่างของ episode คือเกม 1 เกม เล่นจนจบเกม 1 ตาคือ 1 episode
-
ในตัว objective function มันมีพจน์ $P(\tau;\theta)$ ซึ่งเราเคยกระจายออกมาแล้วในสมการที่ \eqref{p-tau} และพบว่าหลัก ๆ มันคือการคูณกันของ $P(s_{t+1}|s_t,a_t)$ และ $\pi_\theta(a|s)$
ตัว $\pi_\theta(a|s)$ เนี่ยไม่มีปัญหาอะไร เนื่องจากว่าเป็น function ที่เรารู้อยู่แล้วว่ามันคำนวณอย่างไร และเราก็สามารถหา derivative มันได้ด้วย (ก็มันคือ neural network เราเอง) แต่ตัวที่มีปัญหาคือ $P(s_{t+1}|s_t,a_t)$ เนื่องจากว่ามันเป็น function การทำงานของ MDP ที่เราไม่รู้ว่ามันทำงานยังไง (อย่างที่เคยบอกไปว่า MDP อาจจะเป็น blackbox แบบนึง ที่เราไม่รู้กระบวนการทำงานข้างใน)
ซึ่งคนที่เค้าคิดค้น Policy Gradient เค้าก็หาทางออกสำหรับปัญหาทั้งสองไว้ให้แล้ว ซึ่งเดี๋ยวจะแสดงเป็น step-by-step ด้านล่าง
-
ก่อนอื่นเราย้าย gradient เข้าไปใน summation ก่อน (ปกติเวลาเราดิฟฟังก์ชันที่มีการบวกกันหลาย ๆ พจน์ เราก็ดิฟแยกพจน์กันอยู่แล้ว)
\[\nabla_\theta \sum_{\tau} P(\tau,\theta)R(\tau) = \sum_{\tau} \nabla_\theta P(\tau,\theta)R(\tau)\] -
ต่อมาเราคูณด้วย 1 เข้าไปซึ่งก็จะไม่มีผลต่อค่าของสมการ แต่ว่า 1 ของเราจะหน้าตาพิเศษ ๆ หน่อยตรงที่ว่ามันเป็น $\frac{P(\tau;\theta)}{P(\tau;\theta)}$
\[\sum_{\tau} \nabla_\theta P(\tau,\theta)R(\tau) = \sum_{\tau} {\color{green}P(\tau;\theta)} \frac{\nabla_\theta P(\tau;\theta)}{\color{green}P(\tau;\theta)} R(\tau)\] -
ซึ่งเราก็จะใช้คุณสมบัติการดิฟ $\frac{dlogx}{dx} = \frac{1}{x}$ และ chain rule มาจัดรูปสมการเป็นดังสมการด้านล่าง
\[\sum_{\tau} P(\tau;\theta) {\color{brown}\frac{\nabla_\theta P(\tau;\theta)}{P(\tau;\theta)}} R(\tau) = \sum_{\tau} P(\tau;\theta) {\color{brown}\nabla_\theta log P(\tau;\theta)} R(\tau)\]ซึ่งขั้นตอนที่ 2 และ 3 มีชื่อเรียกเก๋ ๆ ว่า log derivative trick ซึ่งสำหรับคนที่งงว่าทำไมมันถึงจัดรูปได้แบบนี้ ให้ลองมองย้อนกลับดูว่า $\nabla_\theta log P(\tau;\theta)$ ได้ผลลัพธ์เป็นอย่างไร จะเห็นได้ว่า $log P(\tau;\theta)$ มันเป็น function สองชั้น ซึ่งการหา derivative ของฟังก์ชันในลักษณะนี้ เราก็จะใช้ chain rule
โดยที่
- ชั้นในคือ $P(\tau;\theta)$ ซึ่งเราจะเขียน derivative ของมันเป็น gradient เหมือนเดิมหรือ $\nabla_\theta P(\tau;\theta)$
- และชั้นนอกคือ $log$ ซึ่ง derivative ของ $log x$ ได้ $\frac{1}{x}$ แปลว่าเราจะได้ออกมาเป็น $\frac{1}{P(\tau;\theta)}$
ตาม chain rule เราจะจับ derivative ของทั้งสองชั้นมาคูณกัน เราก็จะได้ว่า
\[\nabla_\theta log P(\tau;\theta) = \frac{\color{blue} \nabla_\theta P(\tau;\theta)}{\color{green} P(\tau;\theta)}\] -
ซึ่งจะสังเกตได้ว่าตอนนี้สมการเราอยู่ในรูปของ summation ของ probability คูณกับ gradient และ reward รวมของ trajectory
\[{\color{green}\sum_{\tau} P(\tau;\theta)} \nabla_\theta log P(\tau;\theta) R(\tau)\]ซึ่งที่จริงมันก็คืออยู่ในรูปแบบของ expected value ของ $\nabla_\theta log P(\tau;\theta) R(\tau)$ นั่นเอง
\[{\color{green}\mathbb{E}_{\tau \sim \pi_\tau}} [\nabla_\theta log P(\tau;\theta) R(\tau)]\]โดยการประมาณค่า expected value นั้น เราอาจจะประมาณมันจาก sample ของ trajectory เท่าที่เราจะหาได้ก็ได้ (เราไม่จำเป็นต้องหาทุก $\tau$ แล้ว ก็เป็นการแก้ปัญหาประการแรกไป) หรือก็คือ
\[\mathbb{E}_{\tau \sim \pi_\tau} [\nabla_\theta log P(\tau;\theta) R(\tau)] \approx \frac{1}{m} \sum_{i = 1}^{m} \nabla_\theta log P(\tau^{(i)};\theta) R(\tau^{(i)})\]ที่จริง log derivative trick ก็เกิดมาเพื่อจัดรูปสมการให้อยู่ในรูปนี้เลย
\[\sum_{type\;of\;fruit} {\color{brown}P(fruit)} weight_{fruit}\]สำหรับคนที่งงว่าทำไมเราถึงประมาณค่ามันด้วย \(\frac{1}{m} \sum_{i = 1}^{m} \nabla_\theta log P(\tau^{(i)};\theta) R(\tau^{(i)})\) ได้ ให้ลองนึกตามนี้
- สมมติว่า เรามีผลไม้ที่คละประเภทกันอยู่ในเรือบรรทุกล้านลูก โดยที่
- ผลไม้แต่ละประเภทเดียวกันจะมีน้ำหนักเท่ากัน ต่างประเภทกันก็จะมีน้ำหนักต่างกัน
- เราไม่สามารถนำทั้งเรือบรรทุกไปชั่งน้ำหนักได้
- ถ้าให้เราหาว่าโดยเฉลี่ยแล้วผลไม้ 1 ผลน้ำหนักเท่าไหร่ ถ้าเรารู้ว่าผลไม้แต่ละประเภทมีเป็น อัตราส่วนเท่าไหร่ใน 1 ล้านลูกนั้น เราก็คำนวณได้ง่าย ๆ เลย
- แต่สมมติว่าถ้าเราไม่รู้ว่าอัตราส่วนของผลไม้แต่ละประเภทเป็นเท่าไหร่ สิ่งที่เราพอจะทำได้ก็คือการ sample ผลไม้ออกมาลังนึง แล้วเอามาหาค่าเฉลี่ยของน้ำหนักของผลไม้ลังนั้น โดยที่เราเชื่อว่าผลไม้ที่มันมีเยอะในเรือบรรทุก มันก็จะมีเยอะใน sample ที่เราหยิบออกมาด้วย
- สมมติว่า เรามีผลไม้ที่คละประเภทกันอยู่ในเรือบรรทุกล้านลูก โดยที่
-
ปัญหาข้อแรกเป็นอันผ่านพ้นไป ปัญหาข้อต่อไปคือตอนนี้เราก็ยังติดค่า $P(\tau;\theta)$ ในสมการอยู่ดี และก็อย่างที่บอกไปว่ามันมีส่วนผสมของค่า $P(s_0)$ และ $P(s_{t+1}|s_t,a_t)$ ซึ่งเป็นส่วนของ environment เราไม่รู้ว่ามันคือค่าอะไร วิธีแก้ก็ง่ายแสนง่าย ณ ตอนนี้ ก่อนอื่นคือให้เราเขียน $P(\tau;\theta)$ ให้อยู่ในรูปของสมการที่ \eqref{p-tau} ก่อน
\[\nabla_\theta log P(\tau;\theta) = \nabla_\theta log\Big{[} P(s_0) \prod_{t=0}^{H} P(s_{t+1}|s_t,a_t) \pi_\theta (a_t|s_t)\Big{]}\] -
ต่อมาให้เราใช้คุณสมบัติ $log(xy) = log(x)+log(y)$ เราก็จะกระจายออกมาได้ดังรูปด้านล่าง
\[{\color{Red} \nabla_\theta log P(s_0)} + {\color{Red} \nabla_\theta \sum_{t=0}^{H}logP(s_{t+1}|s_t,a_t)} + \nabla_\theta \sum_{t=0}^{H} log \pi_\theta (a_t|s_t)\] -
ซึ่งเราจะเห็นได้ว่าพจน์ $ {\color{Red} \nabla_\theta log P(s_0)}$ และพจน์ ${\color{Red} \nabla_\theta \sum_{t=0}^{H}logP(s_{t+1} | s_t,a_t)}$ นั้นไม่ขึ้นอยู่กับตัว $\theta$ เลย มันก็จะเหมือนกับเราดิฟค่าคงที่ได้ 0 เราก็สามารถตัดออกไปได้ให้เหลือแค่
\[\nabla_\theta \sum_{t=0}^{H} log \pi_\theta (a_t|s_t)\]หรือก็คือสมการทั้งหมดของเราก็จะกลายเป็น
\[\frac{1}{m} \sum_{i = 1}^{m} \nabla_\theta log P(\tau^{(i)};\theta) R(\tau^{(i)}) = \frac{1}{m} \sum_{i = 1}^{m} \sum_{t=0}^{H} \nabla_\theta log \pi_\theta(a_t^{(i)}|s_t^{(i)}) R(\tau^{(i)})\]
ตอนนี้เป็นอันว่าเราได้สมการพื้นฐาน Policy Gradient กันมาแล้ว ซึ่งก็คือ
\begin{equation} \label{basic-policy-gradient} \nabla_\theta \sum_\tau P(\tau,\theta)R(\tau) \approx \frac{1}{m} \sum_{i = 1}^{m} \sum_{t=0}^{H} \nabla_\theta log \pi_\theta(a_t^{(i)}|s_t^{(i)}) R(\tau^{(i)}) \end{equation}
แล้วเราก็จะนำ gradient นี้ไปทำ gradient ascent ดังที่แสดงในสมการ \eqref{gradient-ascent} ซึ่งถ้าเรามองแบบ intuitive เลยจะได้ว่า
- ถ้า reward โดยรวมของ trajectory นั้นหรือ $R(\tau)$ มีค่ามาก เราจะพยายามเพิ่ม probability ของทุก action ใน trajectory นั้น
- ถ้า reward โดยรวมของ trajectory นั้นหรือ $R(\tau)$ มีค่าเป็นบวกแต่ไม่มาก เราจะพยายามเพิ่ม probability ของทุก action ใน trajectory นั้นแต่ไม่มาก
- ถ้า reward โดยรวมของ trajectory นั้นหรือ $R(\tau)$ มีค่าเป็นลบ เราจะพยายามลด probability ของทุก action ใน trajectory นั้น
ซึ่งขั้นตอนการนำสมการ \eqref{basic-policy-gradient} ไปใช้ก็จะมี step ง่าย ๆ เลยก็คือ
- ใช้ policy ปัจจุบันไปเก็บประสบการณ์หรือ trajectory มาจาก environment จำนวน $m$ trajectories หรือก็คือ $m$ episodes น่ะแหละ
- คำนวณ gradient ตามสมการที่ \eqref{basic-policy-gradient}
- อัพเดท neural network ด้วย gradient ในข้อที่ 2. เพื่อพัฒนา policy ของเรา
ซึ่งก็เขียนเป็น pseudo code ได้ดังนี้
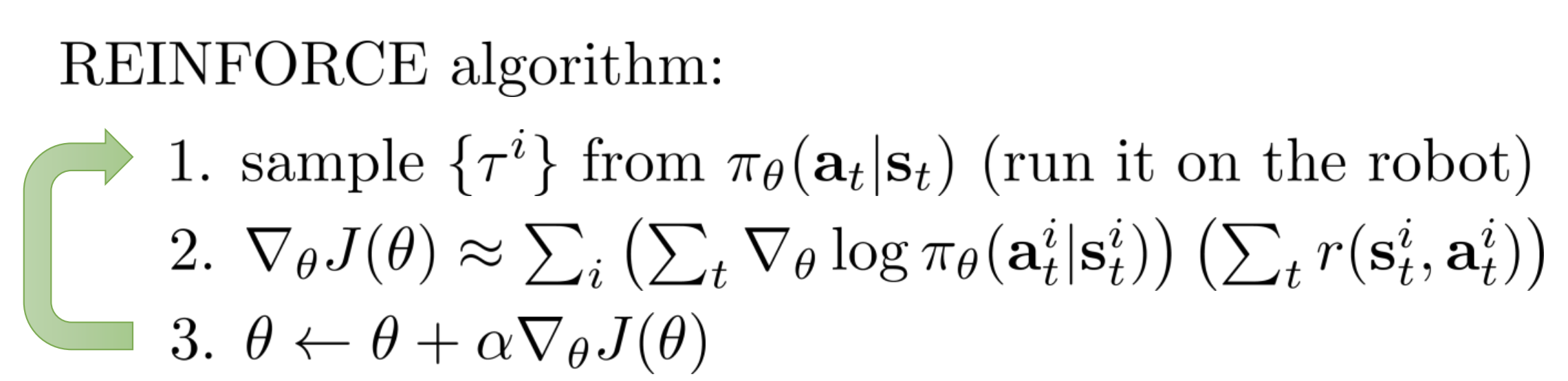 Ref: CS 294-112: Deep Reinforcement Learning, Sergey Levine, Berkeley
Ref: CS 294-112: Deep Reinforcement Learning, Sergey Levine, Berkeley
Reward-to-Go
ตอนนี้เราเอา reward รวมของทั้ง trajectory มาคูณกับ gradient ของทุก action ใน trajectory นั้นซึ่งมันก็แอบแปลก ๆ นิดนึงตรงที่ว่าเราดันไปยกเครดิตจาก reward ที่เกิดก่อนให้กับ action บางตัวที่ทำหลัง reward นั้นซะอีก ดังสมการด้านล่างถ้าคิดดี ๆ จะเห็นว่าเรานำ reward ที่ $t>0$ มาคูณกับ gradient ของ action ที่ $t=0$ ด้วย
\[\frac{1}{m} \sum_{i=1}^{m} \sum_{t=0}^{H} \Bigg{(} \nabla_\theta log\pi(a_t^{(i)}|s_t^{(i)}) \Big{(}\sum_{\color{red} t'=0}^{H} r(s_{t'}^{(i)},a_{t'}^{(i)})\Big{)}\Bigg{)}\]\(R(\tau) = \sum_{t=0}^{H} r(s_{t},a_{t})\) ดังที่แสดงในสมการที่ \eqref{r-tau}
เค้าก็เลยมักจะเปลี่ยนสมการนิดนึงงง ซึ่งเราจะคูณ gradient ของ action ใด ๆ ด้วย summation ของ reward หลังจาก action นั้นเท่านั้น
\[\frac{1}{m} \sum_{i=1}^{m} \sum_{t=0}^{H} \Bigg{(} \nabla_\theta log\pi(a_t^{(i)}|s_t^{(i)}) \Big{(}\sum_{\color{green} t'=t}^{H} r(s_{t'}^{(i)},a_{t'}^{(i)})\Big{)}\Bigg{)}\]ซึ่ง pseudo code เราจะเปลี่ยนไปเป็นดังรูปด้านล่าง
 Ref:Reinforcement Learning: An Introduction (Richard S. Sutton and Andrew G. Barto)
Ref:Reinforcement Learning: An Introduction (Richard S. Sutton and Andrew G. Barto)
จะเห็นได้ว่า
- ในตอนนี้ค่าที่นำไปคูณกับ gradient นั้นจะเป็น summation ของ reward หลัง action นั้น ๆ ซึ่งก็มีการคูณกับ reward discounted factor เพื่อกำหนดให้ reward ในอนาคตมีความสำคัญน้อยกว่าใน reward ในปัจจุบัน
- นอกจากนี้จะเห็นได้ว่าในสมการการอัพเดทค่า $\theta$ นั้น เรามีการคูณ $G_t$ ด้วย $\gamma^t$ อีกทีหนึ่ง เพื่อกำหนดให้ state แรก ๆ ใน trajectory นั้นสำคัญกว่า state ถัด ๆ ไป ถ้าคิดกันแบบบ้าน ๆ ก็คือเค้าให้สำคัญกับจุดเริ่มต้นมากกว่า ถ้าเราเริ่มได้ดี ข้างหลังก็จะดีไปด้วย
ซึ่งการทำ reward-to-go กับการคูณด้วย state discounted factor นั้นจะเป็นการลด variance ของ gradient วิธีหนึ่ง (เขียนรายละเอียดไว้ใน section ข้อด้อยข้างล่าง ว่า variance มันมาจากไหน) ซึ่งจะทำให้เราสามารถเทรน network ได้แบบมีเสถียรภาพและได้ gradient ที่แม่นยำมากขึ้น ซึ่งจะช่วยให้ลู่เข้าสู่ optimal policy ได้เร็ว ๆ
Implementation
ในบทความนี้ก็จะทดลองใช้ policy gradient กับ CartPole environment ให้ดูกันนะครับ
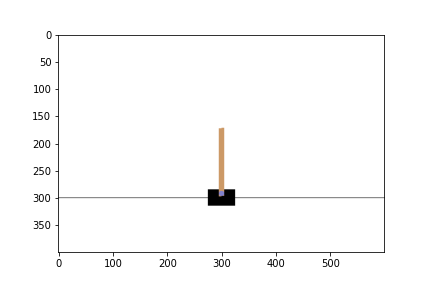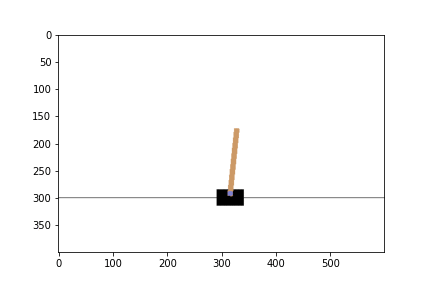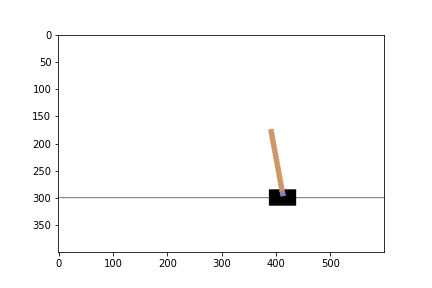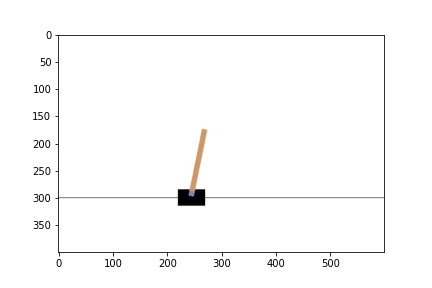
ซึ่ง environment นี้จะให้เราบังคับรถสีดำ ๆ ไปทางซ้ายหรือขวาเรื่อย ๆ เพื่อไม่ให้ท่อนไม้ที่ตั้งอยู่บนรถล้มลงมานั่นเองโดยที่
- State คือ ตำแหน่งของรถ, ความเร็ว, มุมของแท่งไม้, ความเร็วมุมของแท่งไม้
- Action คือขยับไปทางซ้ายหรือขวา
- Reward จะเป็น 1 ในทุก timestep ที่แท่งไม้ยังไม่ล้ม
- Episode จะจบลงต่อเมื่อรถออกนอกเฟรม หรือแท่งไม้เอียงลงมาเกิน 15 องศาจากแนวตั้ง
สำหรับ code เวอร์ชันเต็มสามารถดูได้ที่ colab นี้ครับ
-
เริ่มที่สร้าง environment และเขียนฟังก์ชันสำหรับสร้าง trajectory เตรียมไว้ สังเกตได้ว่าในตอนเลือก action นั้นเราไม่ต้องใช้ epsilon-greedy เหมือนใน Q learning แล้วเพราะว่าการเลือก action ของเราเป็น stochastic policy ซึ่งเราก็สุ่มเลือกในระดับนึง ซึ่งก็นับว่าเป็น exploration อยู่แล้ว
class CartPole: def __init__(self): self.env = gym.make('CartPole-v1') def generate_trajectory(self,agent,render=True): state = self.env.reset() trajectory = [] while True: ## predict probability ของการเลือกแต่ละ action policy = agent(state[np.newaxis,:])[0] ## เลือก action แบบ stochastic policy gradient action = np.random.choice([0,1],p=policy.numpy()) ## ทำ action นั้น next_state,reward,done,_ = self.env.step(action) ## เก็บ trajectory โดยที่เราจะเก็บ log(pi(a|s)) ของ action ที่เราทำเอาไว้เลย history = [state,tf.math.log(policy[action]),reward] if render: history += [self.env.render('rgb_array')] trajectory.append(history) ## ถ้า episode จบแล้ว ก็ให้ break ออกจากลูป if done: break ## ขยับไป state ถัดไป state = next_state return np.array(trajectory) -
ต่อมาเราก็สร้าง neural network กับ optimizer เตรียมไว้
def build_agent(state_size): input_layer = Input(shape = (state_size,)) dense = Dense(100, activation='relu')(input_layer) dense = Dense(100, activation='relu')(dense) dense = Dense(100, activation='relu')(dense) output = Dense(2, activation='softmax')(dense) model = Model(input_layer,output) optimizer = Adam(lr=0.0001) return model,optimizer -
ต่อมาเขียนฟังก์ชันเทรนซึ่งเดี๋ยวเราจะลองใช้ทั้ง reinforce algorithm แบบธรรมดา กับแบบ reward-to-go มาลองดู
-
แบบธรรมดา
def basic_reinforce(env,agent,optimizer): with tf.GradientTape(persistent=True) as tape: trajectory = env.generate_trajectory(agent) log_pi = list(trajectory[:,1]) ## Sum reward ทั้ง trajectory R_tau = np.sum(trajectory[:,2]) ## หา gradient ของ summation ของ log(a|s) ของทุก a และ s ใน trajectory gradient = tape.gradient(log_pi,agent.trainable_variables) ## นำ gradient มาคูณกับ R(tau) ## ปล.สังเกตุว่าเราต้องใส่เครื่องหมายลบไปด้วย เพราะปกติเราคำสั่ง apply_gradient มันจะทำ gradient ## descent ซึ่งเป็นการ minimize แต่เราจะทำ gradient ascent ซึ่งเป็นการ maximize gradient = [-g*R_tau for g in gradient] ## ปรับค่า neural network parameter ด้วย gradient ที่หาไว้ optimizer.apply_gradients(zip(gradient,agent.trainable_variables)) del tape return trajectory ## return list of reward สำหรับเอาไป track ประวัติเฉย ๆ -
แบบ Reward-to-Go
- ก่อนอื่นสร้างฟังก์ชันสำหรับคำนวณ summation ของ reward เพื่อให้เครดิต action แต่ละตัวก่อน ซึ่งก็คือ $G_t = \sum_{k=t}^{H} \gamma^{k-t} r_k$
def cal_Gt(reward_list,gamma=0.99): sum_reward = 0 Gt = [] for reward in reversed(reward_list): sum_reward *= gamma sum_reward += reward Gt.append(sum_reward) return list(reversed(Gt)) print(cal_Gt([1,1,1,0,0])) ## Ouput: [2.9701, 1.99, 1.0, 0.0, 0.0] ## จะเห็นได้ว่า 0,0 สองตัวหลังนั้นคือเราจะไม่ให้เครดิตกับ action 2 สุดท้ายซึ่งเกิดทีหลัง reward 3 ตัวแรก - แล้วก็สร้างฟังก์ชันเทรนด้วย reward-to-go
def reinforce_with_reward_to_go(env,agent,optimizer): with tf.GradientTape(persistent=True) as tape: trajectory = env.generate_trajectory(agent) ## คำนวณ G_t ของแต่ละ timestep Gt = cal_Gt(trajectory[:,2]) ## วนลูปไปทีละ action ใน trajectory for i in range(len(trajectory)): ## หา gradient ของ log pi(a|s) gradient = tape.gradient(trajectory[i,1],agent.trainable_variables) ## คูณ gradient ด้วย Gt gradient = [-g*Gt[i] for g in gradient] ## ปรับ neural network optimizer.apply_gradients(zip(gradient,agent.trainable_variables)) del tape return trajectory
- ก่อนอื่นสร้างฟังก์ชันสำหรับคำนวณ summation ของ reward เพื่อให้เครดิต action แต่ละตัวก่อน ซึ่งก็คือ $G_t = \sum_{k=t}^{H} \gamma^{k-t} r_k$
-
-
หลังจากนั้นเราก็เทรนโลดดด
def train(train_function,max_step=30000): ## สร้าง Environment และ Agent cartpole = CartPole() agent,optimizer = build_agent(4) ## init list เปล่า ๆ ไว้ track ประวัติการเทรน reward_history = {} step = 0 while step<max_step: trajectory = train_function(cartpole,agent,optimizer) reward_history[step] = len(trajectory) step += len(trajectory) return reward_history,agent ## Train history_basic,agent_basic = train(basic_reinforce) history_reward_to_go,agent_reward_to_go = train(reinforce_with_reward_to_go) -
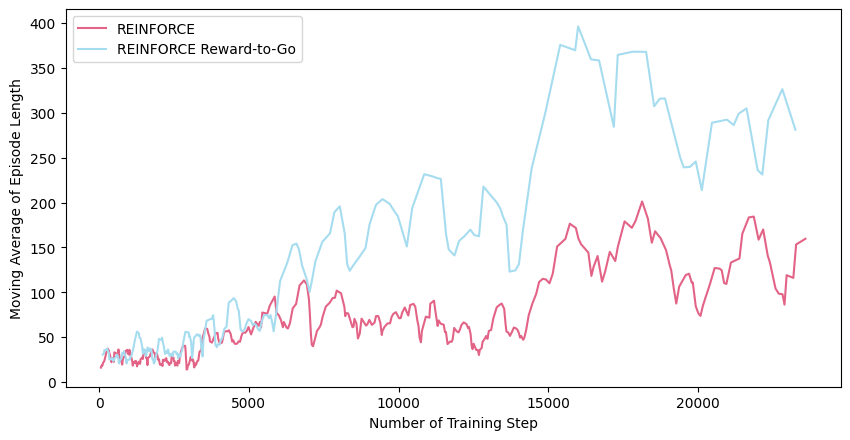
แล้วก็พล็อตผลมาดูจะเห็นได้ว่าในระหว่างการเทรนนั้น episode length นั้นจะเพิ่มขึ้นเรื่อย ๆ ซึ่งก็คือ agent เราสามารถเลี้ยงท่อนไม้ไม่ให้ล้มได้นานขึ้นนั่นเอง ซึ่งจะเห็นได้ว่าการใช้ reward-to-go นั้นสามารถช่วยให้ policy-gradient เรียนรู้ได้เร็วยิ่งขึ้น
ก่อน Train
หลังเทรน
จุดเด่นและจุดด้อยของ Policy Gradient
จุดเด่น
- ที่จริงแล้วมันทำงานกับ continuous action space ได้ ด้วยการที่ให้ neural network เราประมาณค่า mean และ variance ของ action และเราก็สุ่ม action จาก probability density function ที่มี mean และ variance ตามนั้น แต่ว่าในบทความนี้ขออนุญาตไม่พูดถึง เพราะทุกวันนี้ก็ไม่น่ามีใครใช้แล้วมั้ง
-
มันทำงานกับ stochastic policy ซึ่งในบางปัญหามันก็ดีกว่า deterministic policy อย่างเช่นว่า เราจะสร้าง bot ไปเล่นเกมเป่ายิ้งฉุบ ที่ optimal policy คือการออกค้อน กรรไกร กระดาษด้วย probability เท่า ๆ กัน เพราะถ้าเราใช้ deterministic policy เราอาจจะถูกอีกฝ่ายจับทางได้
แต่ว่าถ้าปัญหาไหนที่มันต้องการ deterministic policy ตัว policy gradient เราจะค่อย ๆ ปรับ probability ของ optimal action ไปให้ใกล้ ๆ 1 หรือก็คือปรับไปจนเป็น deterministic policy ไปให้เอง อย่างเช่นตัวอย่างด้านล่าง เราลองใช้ policy gradient กับปัญหาง่าย ๆ คือเริ่มที่ตรงกลาง ถ้าเดินไปทางขวาจนสุดจะได้ reward +1 แต่ถ้าเดินไปทางซ้ายจนสุดจะได้ reward -1 จะเห็นได้ว่าเมื่อเทรนไปเรื่อย ๆ ค่า probability ของการเดินไปทางขวานั้นจะเข้าใกล้ 1 มากขึ้นเรื่อย ๆ
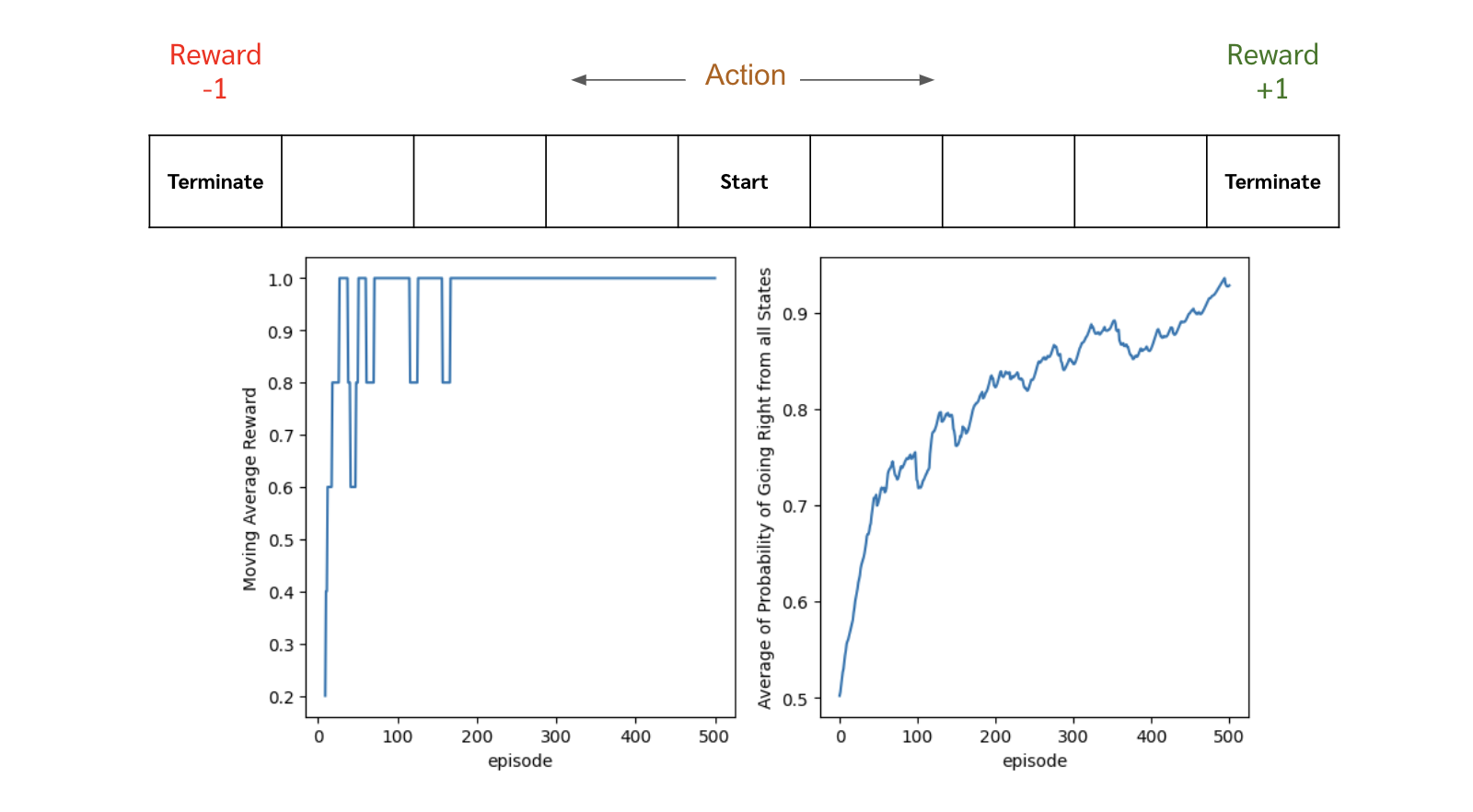
จุดด้อย
-
ไม่การันตี global optimal policy ซึ่งเป็นเพราะว่าเราใช้ตัว gradient ascent ในการทำ มันอาจจะไปหยุดอยู่ที่ local optimal policy ตรงไหนก็ได้ ซึ่งแตกต่างจากพวกตระกูล Q-learning ที่มันการันตีตัว global optimal policy ถ้าเรา visit ครบทุก state และลองทำทุก action มากพอ (ซึ่งจริง ๆ เป็นไปได้ยากอยู่ดีแหละ)
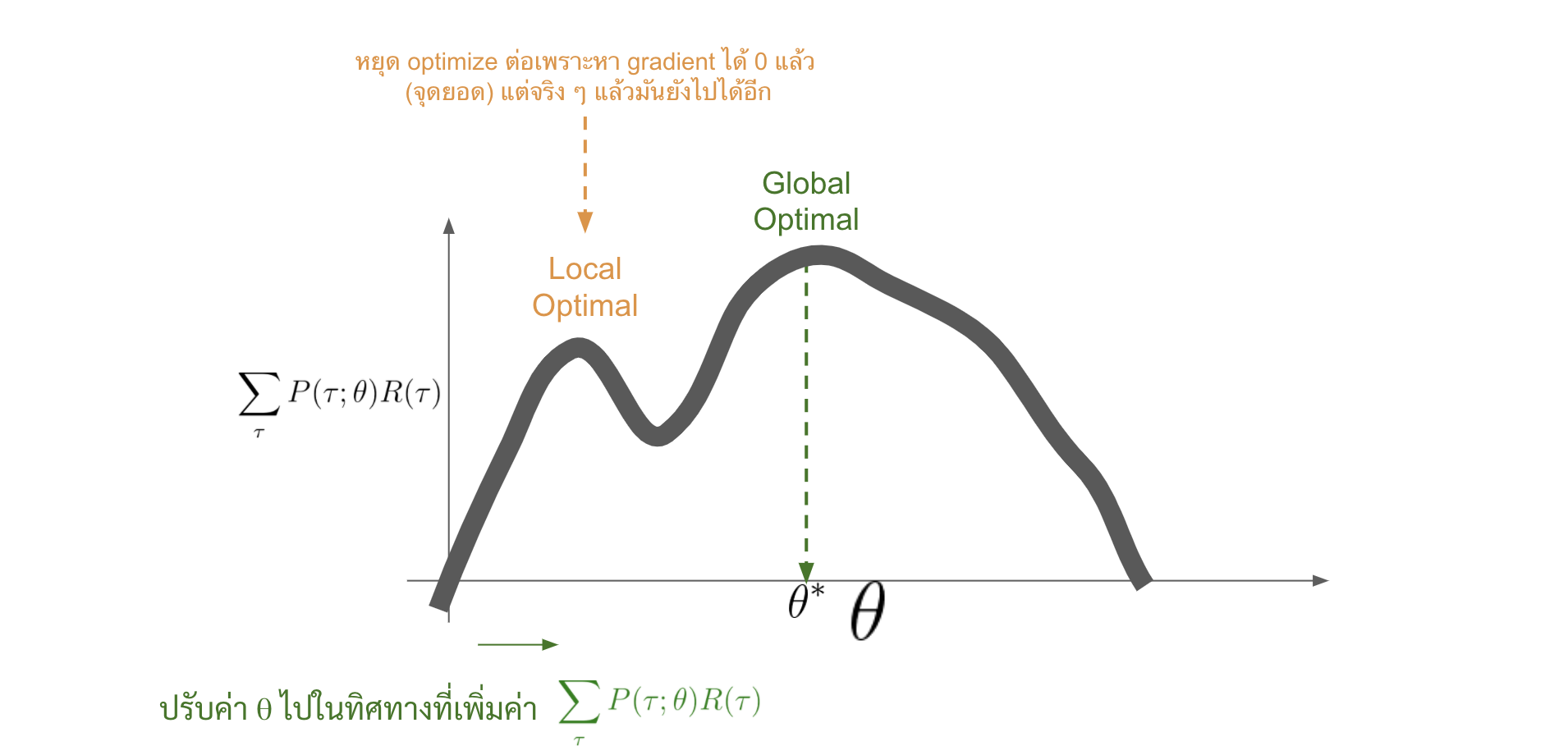
-
ใช้ experience เปลือง ไม่สามารถ reuse experience เก่า ๆ มาอัพเดท neural network ใหม่ได้ เนื่องจากว่า policy ในอดีตกับ policy ในปัจจุบันที่เรากำลัง optimize มันอยู่เนี่ย มันจะมี behaviour ไม่เหมือนกันแล้ว ซึ่งก็จะส่งผลให้ค่า $P(\tau;\theta)$ ไม่เหมือนกัน ซึ่งถ้ายังจำกันได้เราบอกว่าค่าที่เราจะ optimize เนี่ยมันคือ
\[\sum_{\tau} {\color{red}P(\tau;\theta)} R(\tau)\]ซึ่งถ้า $\theta$ เปลี่ยนไป ตัวฟังก์ชัน \(\sum_{\tau} P(\tau;\theta) R(\tau)\) นี้ก็จะอยู่กันคนละค่า หรือคนละที่ ค่า gradient ก็จะแตกต่างกันไปด้วย
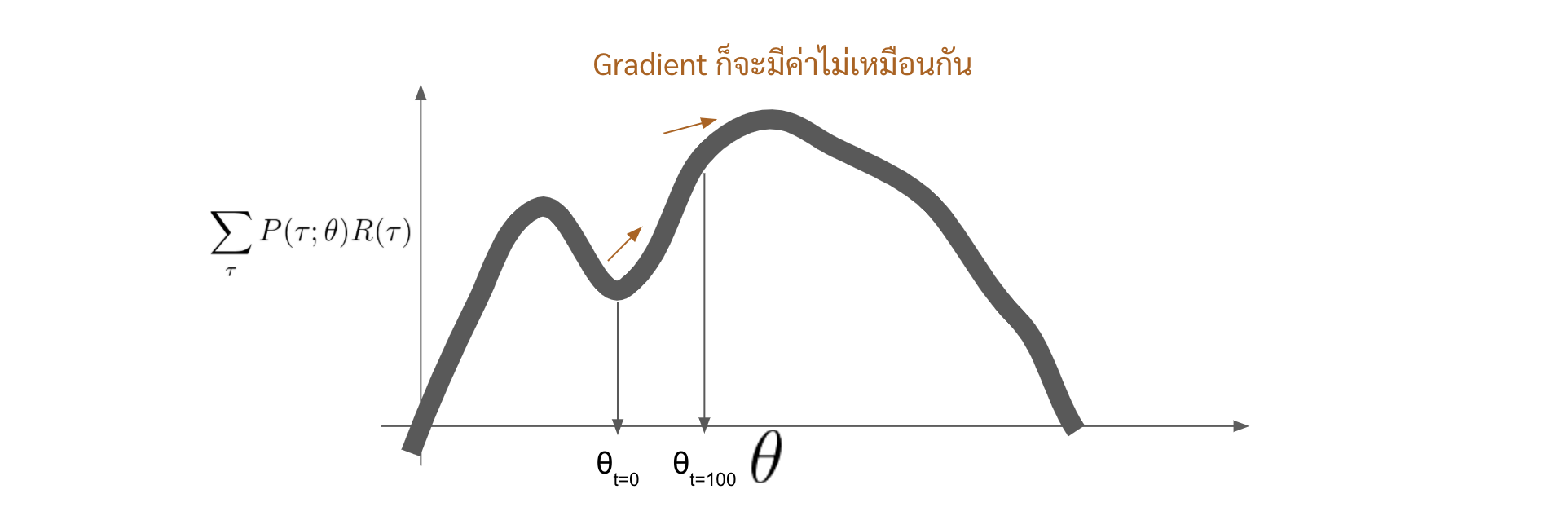
หรือก็คือ experience ที่เก็บมาด้วย policy เก่า ๆ มันตกยุคไปแล้ว หรืออย่างเช่นว่า ใน policy เมื่อ 100 episodes ที่แล้วเราอาจจะไป trajectory นึง แต่ในปัจจุบันเราเรียนรู้จนเราไปในอีกทางนึงอย่างสิ้นเชิงแล้ว เราจะเอา experience ของเมื่อ 100 episodes ที่แล้วมาก็จะแปลกๆหน่อย ที่จริงคือไม่ได้เลยแหละ
-
variance ของการเทรนสูง เนื่องจากว่าตอนนี้เราคูณ gradient ด้วย summation ของ reward ของ trajectory ล่าสุด
\[\nabla_\theta log \pi_\theta(a_t|s_t) {\color{red}R(\tau)}\]ซึ่งสมมติว่า trajectory มันยาวในระดับหนึ่ง และ reward แต่ละตัวก็สุ่มมาจาก distribution อะไรซักอย่าง แล้วเราเอา reward ทุกตัวมาบวกกันหมดเลย สิ่งที่เกิดขึ้นคือ variance มันจะกว้างมาก (variance จะเท่ากับ variance ของ reward แต่ละ timestep บวกกัน) และเมื่อ variance มันกว้างมาก สมมติเราได้ trajectory ที่ได้ summation ของ reward อยู่ขอบ ๆ ของ distribution เลย gradient ในการอัพเดทรอบนั้นจะทรงพลังมาก ซึ่งอาจจะ dominate การอัพเดทก่อนหน้าไปหมดเลยก็ได้
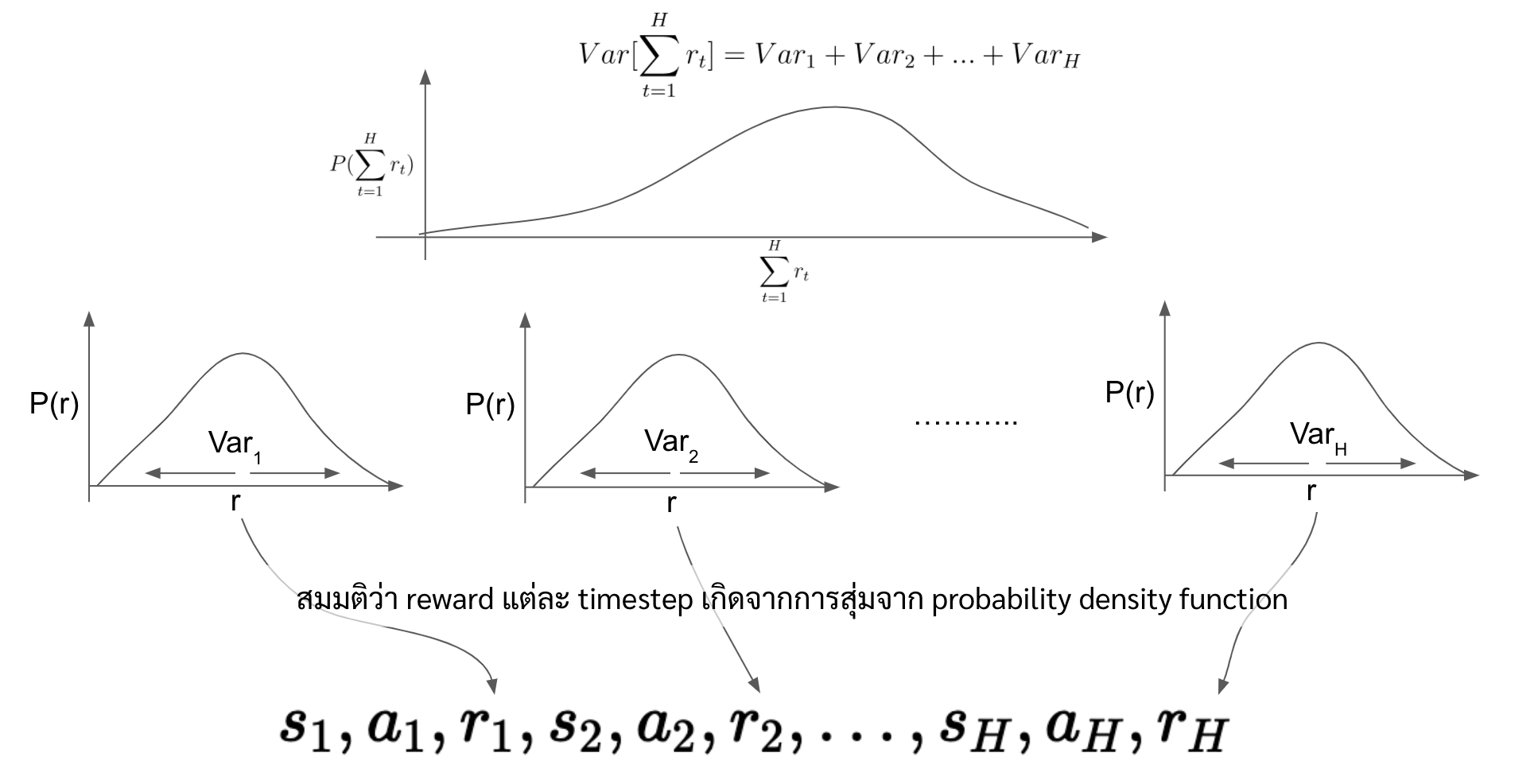
ถ้าใครนึกภาพตามไม่ออก ให้ลองคิดว่าแบบนี้สมมติเรามี reward สามตัว ทั้ง 3 ตัวจะถูกสุ่มมาจาก distribution ตัวนึงที่มี min เป็น -10 และ max เป็น +10 ก็แปลว่า reward รวมทั้งสามตัวน้อยที่สุดที่เป็นไปได้คือ -30 ในขณะที่มากที่สุดที่เป็นไปได้คือ +30 ซึ่งถ้าเรายิ่งเพิ่มจำนวน reward เข้าไป range ของ 2 ค่านี้ก็จะกว้างขึ้นเรื่อย ๆ
แต่ว่าก็มีวิธีในการลด variance อยู่ เช่น การลบกับ baseline ที่เป็น state value หรือการใช้ actor-critic ที่เราใช้ neural network อีกตัวมาประมาณค่า cumulative reward ให้แทนที่จะใช้ summation จาก trajectory ปัจจุบัน ซึ่งถ้ามีโอกาสจะมาเขียนให้อ่านกันครับ ที่จริงตอนแรกก็กะจะเขียนในบทความนี้เลย แต่เขียนไปเขียนมายาวเกิน เลยขอตัดจบไปก่อน
Disclaimer
รายละเอียดในบทความนี้มาจากความเข้าใจส่วนตัว อาจมีข้อผิดพลาด หากพบจุดผิดพลาด ขอความกรุณาแจ้งทาง facebook หรือ email: thammasorn.han@hotmail.com