Multi-Armed Bandit คืออะไร?

k-armed bandit เป็นโจทย์ปัญหาที่พื้นฐานที่สุดของ reinforcement learning เพราะมีเพียงแค่ state เดียวและ agent เพียงต้องพยายามประมาณให้ได้ว่า reward ที่ได้จากแต่ละ action เป็นเท่าใด โดยที่ปัญหามีอยู่ว่า

มีตู้กดอยู่ k ตู้ และเราต้องเลือกว่าจะกดที่ตู้ไหน เมื่อกดไปที่ตู้ใดแล้ว ตู้นั้นจะสุ่มค่ารางวัลออกมาให้ ซึ่งแต่ละตู้จะมีค่าเฉลี่ยของรางวัลแตกต่างกัน เช่น ตู้ที่หนึ่งมีค่าเฉลี่ยของรางวัลคือ 10, ตู้ที่สองมีค่าเฉลี่ยของรางวัลคือ 20 ฯลฯ แต่ค่าเฉลี่ยเหล่านี้เราไม่รู้

โจทย์คือจะทำอย่างไรให้เราสามารถสะสม reward ให้ได้มากที่สุดเมื่อเล่นไปนาน ๆ (กดตู้ทั้งหมด 100 ครั้ง 1000 ครั้ง→ infinite ครั้ง)

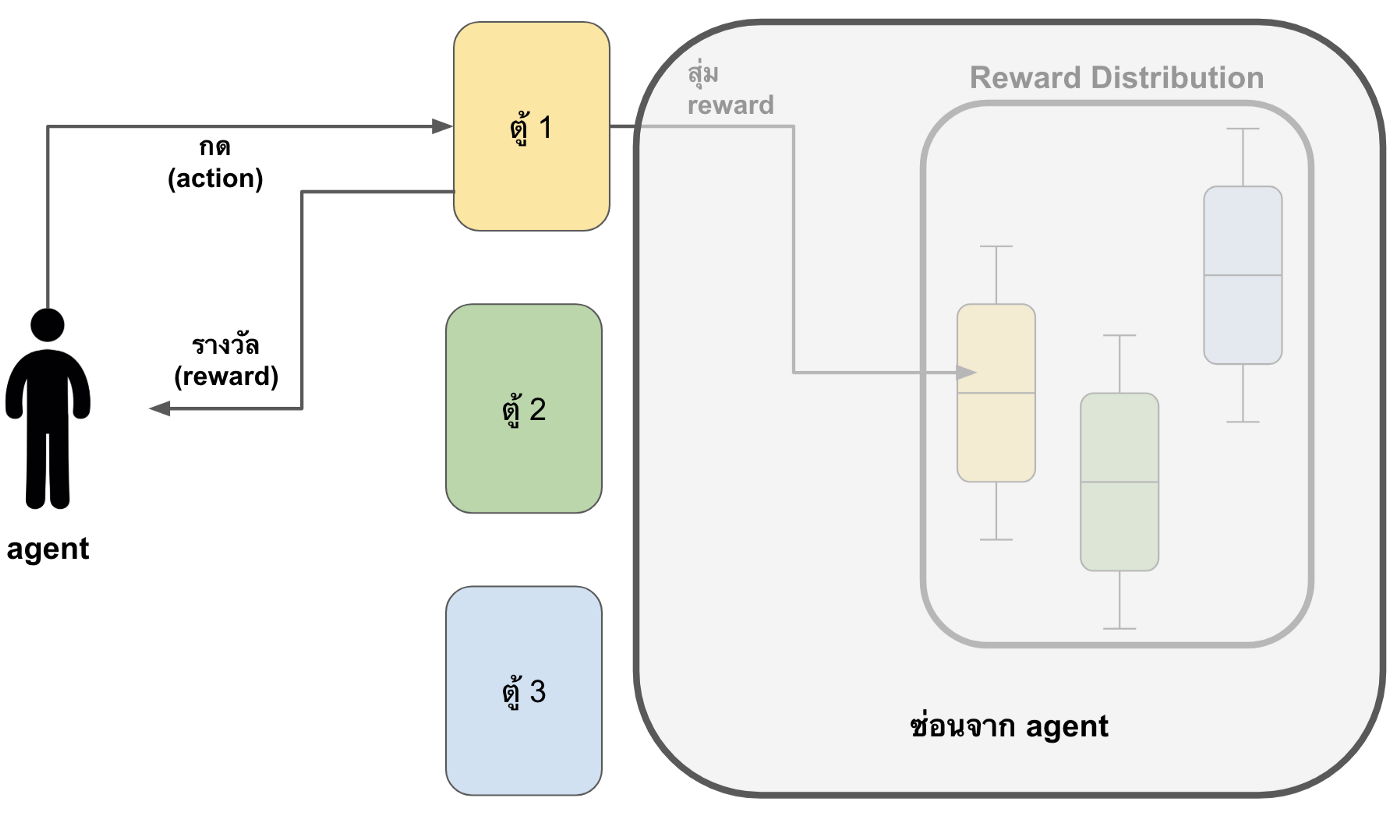
เราสามารถมองปัญหา k-armed bandit เป็น reinforcement learning ได้ดังนี้

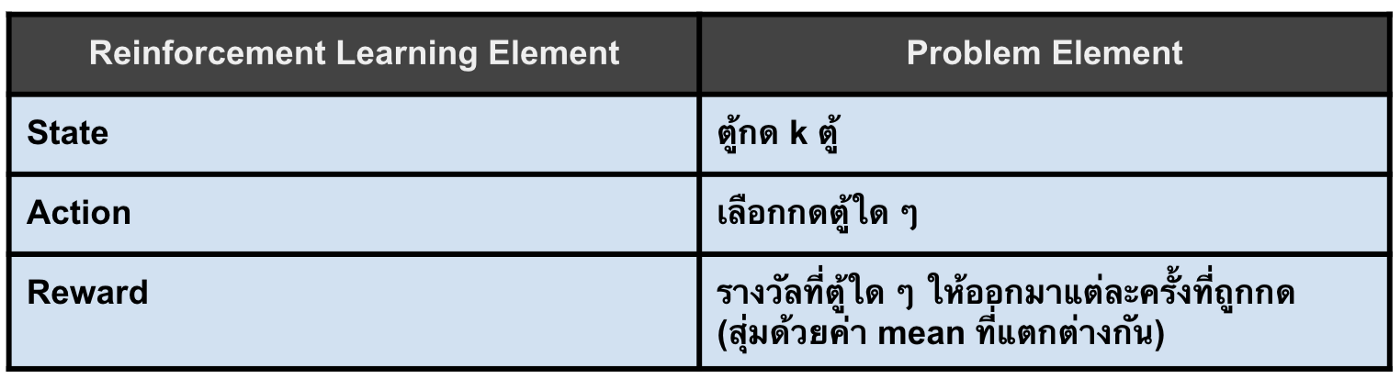
ซึ่ง k-armed bandit นั้นเป็นปัญหาที่มีแค่ state เดียวคือ การที่ agent ต้องเผชิญหน้ากับตู้กดจำนวน k ตู้ และมีจำนวน action เป็น k actions ซึ่งก็คือจำนวนตู้ให้เลือกกด ในส่วนของ reward ก็คือจำนวนรางวัลที่แต่ละตู้สุ่มมาให้เมื่อถูกกด

การแก้ปัญหา Multi-Armed Bandit

ดังที่กล่าวไปข้างต้นว่าแต่ละตู้กดนั้นจะมีค่าเฉลี่ยของรางวัลที่แตกต่างกัน บางตู้มาก บางตู้น้อย เพราะฉะนั้นการแก้ปัญหา k-armed bandit นั้นคือการทำให้เราสามารถหาได้ว่าตู้กดใดที่มีค่าเฉลี่ยของรางวัลที่มากที่สุด แต่ว่าระหว่างที่กำลังค้นหาว่าตู้ไหนมีค่าเฉลี่ยรางวัลมากที่สุด agent จะต้องสะสม reward ให้ได้มาก ๆ ด้วย

เราจะเรียกค่าเฉลี่ยของรางวัลของแต่ละตู้ว่า action value เหตุผลที่เรียกว่า action value ก็เพราะว่ามันคือค่าเฉลี่ยของ reward ที่เราจะได้จากการทำแต่ละ action จะใช้ตัวย่อเป็น $q^\ast(a)$ เมื่อ $a$ คือ action หรือตู้ที่เลือกกด

\begin{equation} \label{eq:q} q^\ast (a) = \mathbb{E}[R_t | A_t = a] \end{equation}

สมการที่ \eqref{eq:q} สามารถแปลความหมายง่าย ๆ ว่า $q^\ast(a)$ คือค่าความคาดหวังของ reward เมื่อเราทำ action $a$ ณ เวลา $t$

ถ้าเรารู้ $q\ast(a)$ แต่แรกก็จบ เพราะเราก็แค่เลือกแต่ตู้ที่มีค่า $q\ast(a)$ สูงที่สุด แต่ปัญหาคือเราไม่รู้นี่สิ

เพราะฉะนั้นสิ่งที่เราต้องทำคือในตอนแรกเราจะลองผิดลองถูกเลือกแบบสุ่มไปก่อน แต่ทุกครั้งที่เรากดเลือกตู้ใด ๆ เราจะทำการประมาณค่า $q\ast (a)$ ของตู้นั้น ๆ ด้วยค่าเฉลี่ยของ reward ที่ได้มาก่อนหน้าเมื่อเรากดตู้นั้น ๆโดยค่าประมาณนี้จะแทนด้วย $Q_t(a)$ เมื่อ $t$ คือลำดับครั้งที่เรากดตู้

\begin{equation} \label{eq:Qt} Q_t(a) = \frac{ผลรวมของรางวัลที่ได้จากการกดตู้ \ a \ จากการกดตู้ทั้งหมด \ t-1 \ ครั้ง}{จำนวนครั้งที่กดตู้ \ a \ จากการกดตู้ทั้งหมด \ t-1 \ ครั้ง} \end{equation}

ตัวอย่างการคำนวณค่า Qt(a) เนื่องจากในตอนนี้เรายังไม่มี policy เพราะฉะนั้นในตารางด้านล่างเราจะสมมติว่าเลือก action ด้วยการสุ่มแบบ uniformly distributionโดยที่ reward มาจากการสุ่มจาก reward distribution ของแต่ละเครื่อง

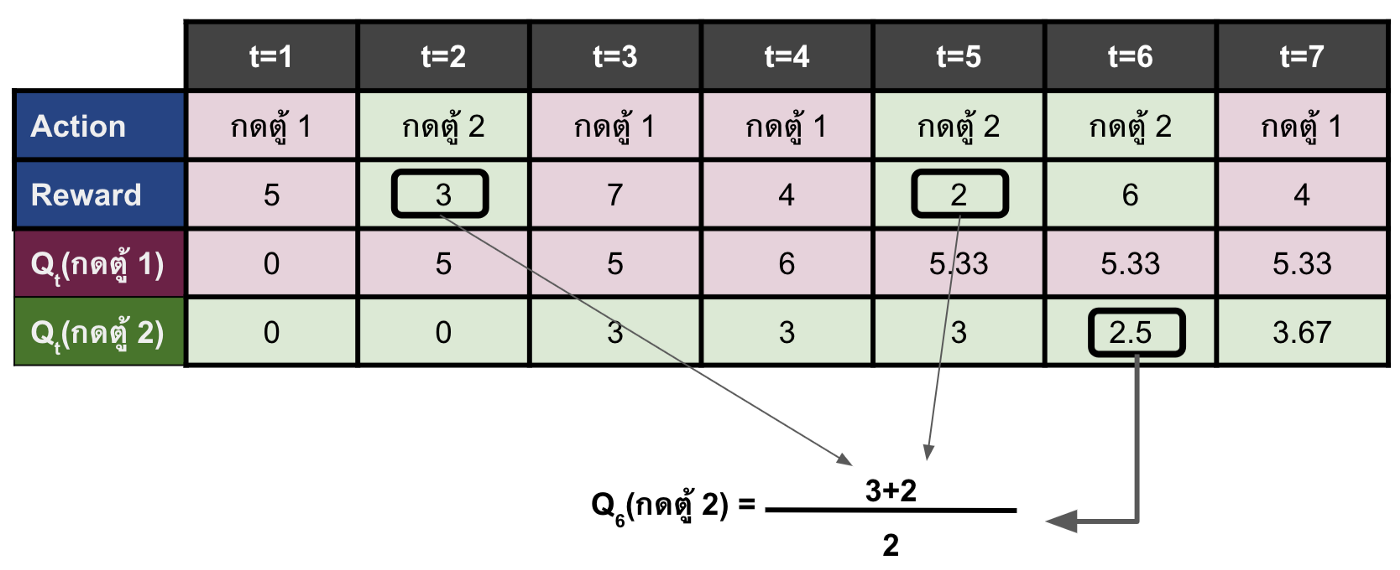
เพราะฉะนั้นแล้วยิ่ง $t$ สูงหรือเวลาผ่านไปนานนั้นหมายความว่าสมการด้านบนจะมี จำนวน sample ที่มากขึ้นในการหาค่าเฉลี่ย ซึ่งจะทำให้ค่า $Q_t(a)$ ค่อย ๆ ลู่เข้าใกล้ค่า $q^\ast(a)$ มากขึ้นเรื่อย ๆ

อย่างไรก็ตามต้องอย่าลืมว่าเป้าหมายหลักของเราจริง ๆ แล้วไม่ใช่แค่การประมาณค่า $q^\ast(a)$ แต่เราจะต้องสะสม reward ให้ได้มากที่สุดอีกด้วย ทำให้คำถามต่อมาของเราคือ ในระหว่างที่เราลองผิดลองถูก เราจะเลือกตู้ที่จะกดหรือจะมี policy อย่างไร เพื่อทำให้ได้ reward มาก ๆ ควบคู่ไปกับการประมาณค่า $Q_t(a)$ ด้วย

คำตอบคือเราสามารถนำค่า $Q_t(a)$ มาใช้ในการสร้าง policy ได้ โดย policy ที่ง่ายที่สุดคือในแต่ละเวลา $t$ นั้น เราจะเลือก action ที่มีค่า $Q_t(a)$ มากที่สุด เราจะเรียก policy แบบนี้ว่า greedy policy ถ้าจำง่าย ๆ ก็คือ greedy แปลว่าโลภ ซึ่งก็เหมือนกับ policy เราที่จะเลือกแต่ค่าที่ให้ $Q_t(a)$ มากที่สุด

\begin{equation} \label{eq:greedy_policy} Action = argmax_a (Q_t(a)) \end{equation}

ฟังดูเผิน ๆ เหมือนจะดี แต่จริง ๆ ไม่ใช่ เนื่องจากการใช้เพียง greedy policy จะทำให้มีโอกาสที่เราจะเลือกเพียง action เดียว ซึ่งจะทำให้ค่า $Q_t(a)$ ของ action อื่น ๆ ไม่ได้ถูกประมาณให้ใกล้เคียงกับค่า $q^\ast(a)$ มากขึ้นเลย ทำให้เราไม่รู้ว่าจริง ๆ แล้ว action อื่นดีแค่ไหน เพราะเรามัวแต่ทำ action เดิม

ดังในรูปด้านล่างที่จริงแล้ว \(q^\ast(กดตู้2)\) อาจจะมีค่ามากกว่า \(q^\ast(กดตู้ 1)\) ก็ได้ แต่ในครั้งแรกเราทำการสุ่มเลือก action และเลือกตู้ 1 มาทำให้ตู้ 1 มี $Q_t$ มากกว่าตู้ 2 หลังจากนั้น เราเลยไปเลือกแต่ตู้ 1 ทั้ง ๆ ที่ไม่เคยประมาณค่า \(q^\ast(กดตู้ 2)\) ด้วยซ้ำไป

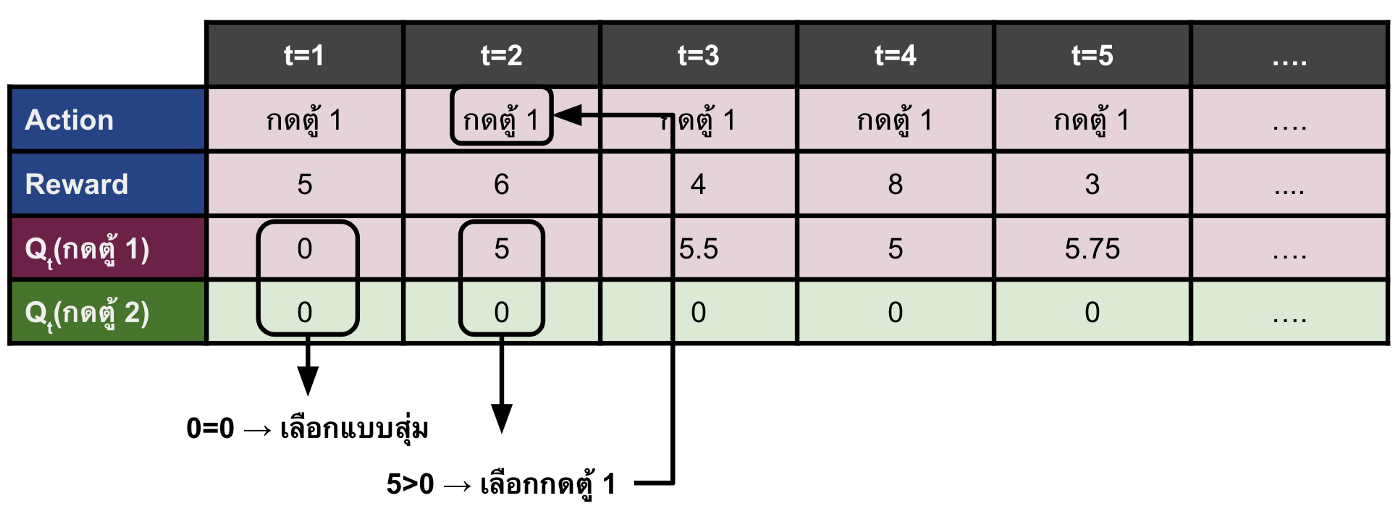
เพราะฉะนั้นการเลือกกดตู้ใด ๆ นั้น เราเลือกกดแต่ตู้ที่มีค่า Qt(a) มากที่สุดเพียงอย่างเดียวไม่ได้ ในบางครั้งต้องลองเลือกกดตู้อื่นบ้าง เพื่อเป็นการทดลองหาทางเลือกใหม่ ๆ ที่อาจจะดีกว่าเก่า เราเรียกกว่าทำเช่นนี้ว่า exploration ที่แปลว่าการสำรวจ มันคือการออกไปนอกกรอบหาอะไรใหม่ ๆ ที่อาจจะดีกว่าเดิม

สรุปให้เข้าใจง่ายอีกทีก็คือ กระบวนการเลือก action ของเราจะประกอบด้วย 2 วิธีหลัก ๆ ได้แก่

• เลือก action ที่มี $Q_t(a)$ มากที่สุด การเลือกแบบนี้เรียกว่า exploitation โดยที่วิธีนี้จะช่วยในการสะสม reward ให้ได้มากที่สุด เนื่องจากเป็นการเลือกสิ่งที่ดีที่สุดโดยพิจารณาจากข้อมูลที่มีอยู่ หรือประสบการณ์ก่อนหน้า
• เลือก action ทั้งหมดด้วยความน่าจะเป็นที่เท่ากันหมดโดยไม่สน $Q_t(a)$ การเลือกแบบนี้เรียกว่า exploration ซึ่งจะช่วยทำให้ค่า $Q_t(a)$ ของทุก action ใกล้เคียงกับ $q^\ast(a)$ มากขึ้น เพราะการทำ exploration นั้นช่วยการันตีว่าทุก action มีความน่าจะเป็นที่จะถูกเลือกมาทำ ทำให้แต่ละ action มี sample มากพอที่จะสามารถคำนวณสมการ $Q_t(a)$ ด้านบนให้ได้ผลใกล้เคียงกับ $q^\ast(a)$ ได้มากขึ้น ซึ่งการทำแบบนี้จะช่วยให้ exploitation สามารถเลือก action ที่ดีที่สุดได้อย่างแม่นยำมากยิ่งขึ้น (อย่าลืมว่า exploitation คือการเลือก action ที่ให้ค่า $Q_t(a)$ มากที่สุด เพราะฉะนั้นยิ่งค่า $Q_t(a)$ แม่นยำมากเท่าไหร่ ก็จะสามารถเลือก action ที่แม่นยำมากขึ้นเท่านั้น)

เมื่อเรารู้ว่าควรมีวิธีการเลือก action สองแบบแล้ว คำถามถัดมาคือแล้วเมื่อไหร่เราควรจะเลือกแบบ exploitation เมื่อไหร่ควรจะเลือกแบบ exploration ซึ่งวิธีแก้ปัญหานี้คือเราจะตั้งค่าความน่าจะเป็นมาหนึ่งค่าและแทนด้วย $\epsilon$

• เลือก action แบบ exploration ภายใต้ความน่าจะเป็น $\epsilon$
• เลือก action แบบ exploitation ภายใต้ความน่าจะเป็นที่เหลือ (1-$\epsilon$)

วิธีนี้เราเรียกว่า epsilon greedy

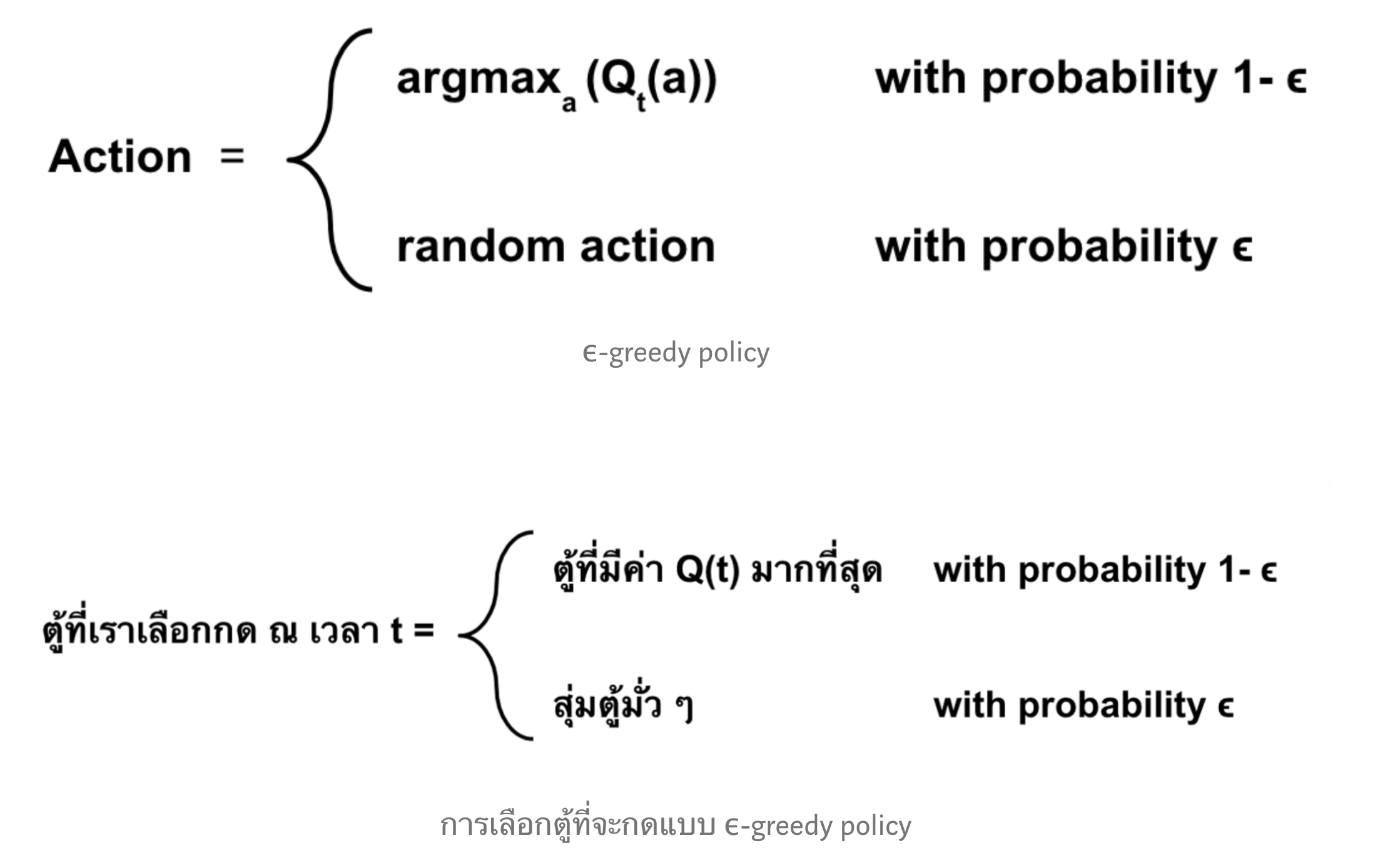
แล้วเราจะรู้ได้อย่างไรว่าค่า $\epsilon$ ควรเป็นเท่าไหร่ดี ถ้าเราลองคิดเล่น ๆ จะพบว่าค่า $\epsilon$ บ่งบอกถึงความบ่อยของ exploration และจากด้านบนบอกว่า exploration ช่วยทำให้ค่า $Q_t(a)$ ลู่เข้าสู่ค่า $q^\ast(a)$ ของทุก action ได้เร็วมากขึ้น เพราะฉะนั้น

$\epsilon$ สูงจะทำให้ agent เรามีโอกาสที่จะพบ action ที่ดีที่สุดได้เร็วขึ้น

แต่ก็ใช่ว่าค่า $\epsilon$ สูงจะดีเสมอไป อย่าลืมว่าค่า $\epsilon$ สูงจะทำให้การทำ exploitation น้อยลง ซึ่งส่งผลให้ reward สะสมตลอดนั้นน้อยลงไปด้วย เพราะแทนที่เราจะไปเลือก action ที่มีค่า value function เยอะ ๆ นั้น เราดันไป explore ซะมากกว่า

$\epsilon$ มากจะทำให้ความน่าจะเป็นที่เลือก action ที่เป็น optimal action นั้นน้อยลง

A simple Bandit Algorithm

เราสามารถสรุป algorithm ที่ใช้ในการแก้ปัญหา k-armed bandit ได้ดังรูปด้านล่าง

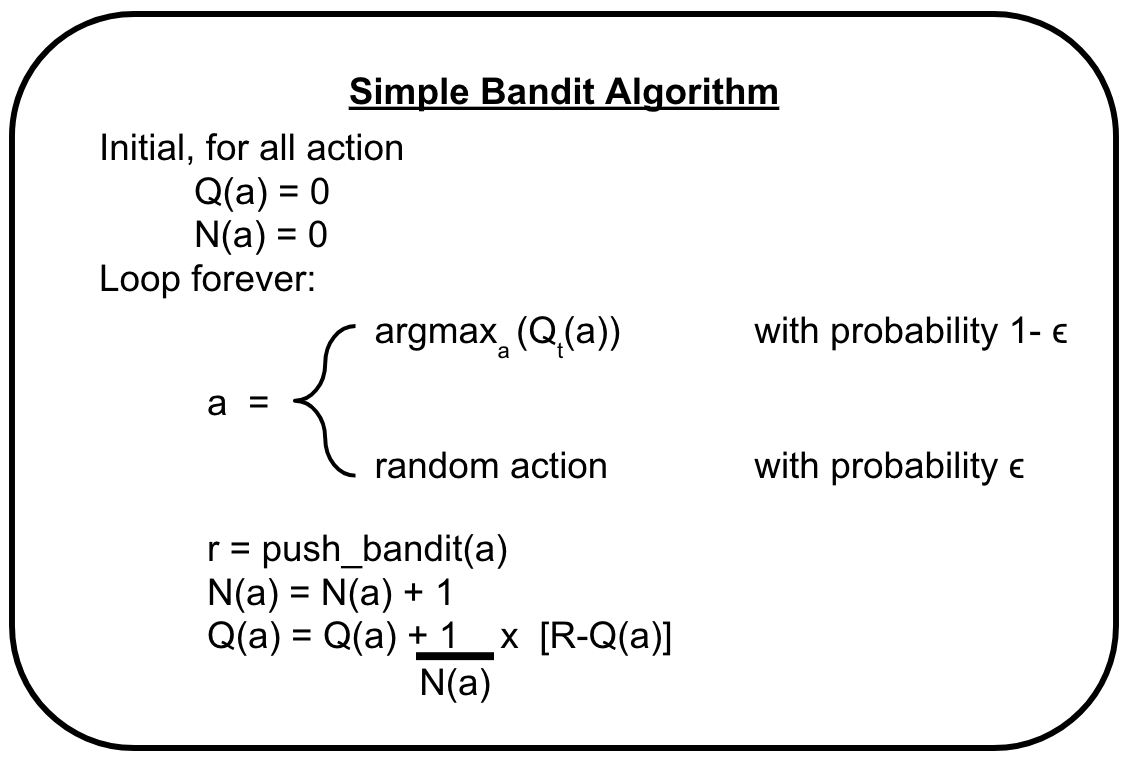
ซึ่งสามารถอธิบายได้ดังนี้

1. ตั้งค่า $Q(a)$ และ จำนวนครั้งในการถูกเลือก( $N(a)$ ) ของทุก action เป็น 0
2. ให้ agent ใช้ $\epsilon$-greedy policy เลือก action หรือตู้ที่จะกด (แทนด้วย $a$)
3. เมื่อเลือก action และไปกดตู้แล้ว สิ่งที่ได้ออกมาคือ reward ที่ตู้นั้นสุ่มให้ แทนด้วย $r$
4. บันทึกจำนวนครั้งที่เราเลือกกดตู้ $a$ ด้วยการบวก $N(a)$ เพิ่มขึ้น 1
5. Update ค่า $Q(a)$ ใหม่ ด้วย reward ที่เพิ่งได้รับมา (สมการในรูปด้านล่างแตกต่างจากสมการ $Q_t(a)$ ที่ได้นำเสนอไปด้านบน แต่ทั้งสองสมการนั้นสามารถหาค่า $Q_t(a)$ ได้ประมาณกัน)
6. ทำตั้งแต่ขั้นตอนที่ 2 ถึง 5 ใหม่ ซ้ำ ๆ ไปเรื่อย ๆ ในที่สุดค่า $Q(a)$ ของทุก a จะลู่เข้าค่า $q^\ast(a)$

ทดลอง

ปัญหา

• มี 3 ตู้ โดยที่แต่ละตู้มีค่าเฉลี่ยรางวัลหรือ q*(a) เท่ากับ 20, 40 และ 80 ตามลำดับ โดยที่มี variance ของรางวัลเท่ากับ 20
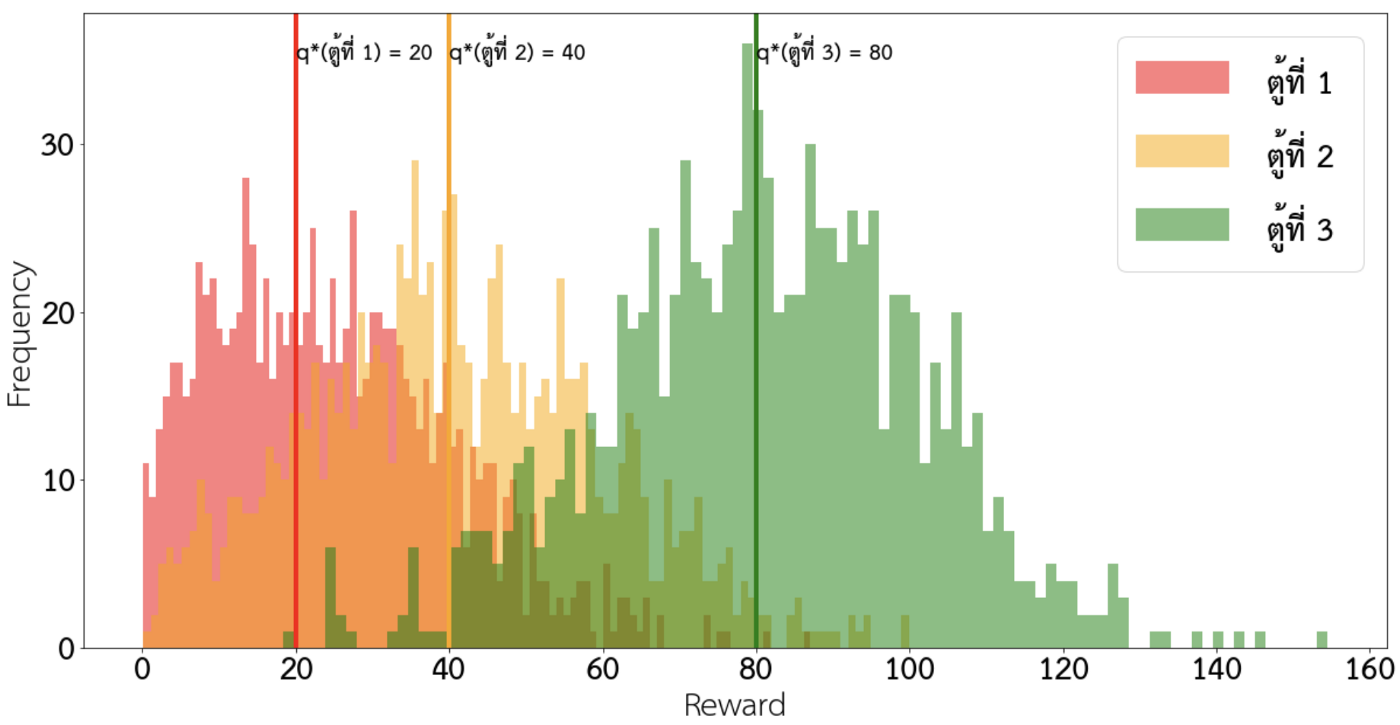
• ให้ agent ได้เลือกกดตู้ทั้งหมด 4,000 ครั้ง
• ทดลองพัฒนาด้วย ϵ-greedy policy ที่มีค่า ϵ=0.01 และ 0.1

ผลการทดลอง

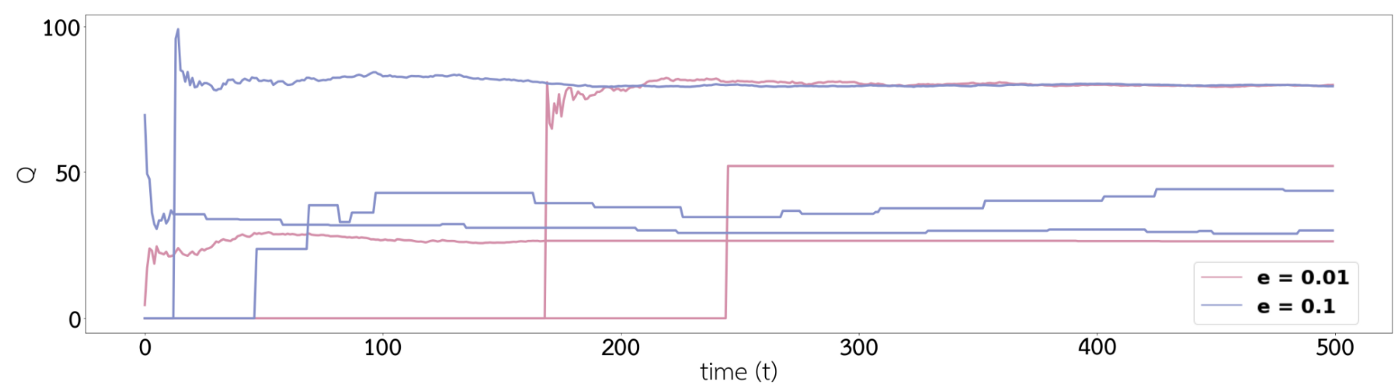
กราฟด้านบนนั้นเปรียบเทียบค่า $Q_t(a)$ เมื่อเวลาผ่านไป ทั้งสีฟ้าและสีชมพูจะมีสีละ 3 เส้นแทนค่า $Q_t(a)$ ของแต่ละตู้ จะเห็นได้ว่าค่า $Q$ ของสีฟ้านั้น stable อยู่ที่ค่า 20 40 และ 80 ( $q\ast(a)$ ตามโจทย์) ได้เร็วกว่าสีชมพู เป็นไปตามที่เราคิดกันไว้ข้างบนว่ายิ่งมีค่า $\epsilon$ สูงจะทำให้ค่า $Q_t(a)$ สามารถลู่เข้า $q^\ast(a)$ ได้เร็วยิ่งขึ้น

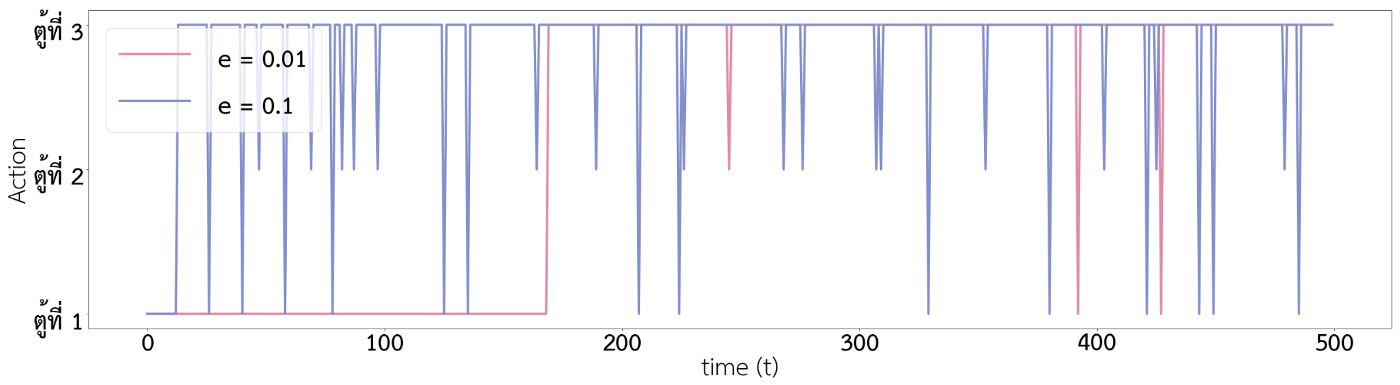
จากกราฟด้านบนจะเห็นได้ว่า เส้นสีฟ้านั้นไปกดตู้ 3 บ่อย ๆ ตั้งแต่เวลาประมาณ $t=10$ นิด ๆ ซึ่งเร็วกว่าเส้นสีชมพูที่กว่าจะไปเลือกกดตู้ 3 บ่อย ๆ ก็ปาไปเวลา $t=170$

นั่นเป็นเพราะว่า สีฟ้ามีค่า $\epsilon$ มากกว่าสีชมพู จึงทำให้ค่า $Q_t(a)$ ของสีฟ้าลู่เข้าสู่ค่า $q^\ast(a)$ ได้เร็วกว่า และทำให้สามารถพบ action ที่ดีที่สุดได้เร็วกว่าสีชมพู แต่หลังจากที่สีชมพูค้นพบ action ที่ดีที่สุดบ้างแล้ว ($t=170$ เป็นต้นไป) สีชมพูมีความคงที่ของการเลือกกดตู้ 3 มากกว่าเส้นสีฟ้า เนื่องจากสีฟ้ามีค่า $\epsilon$ ที่มากกว่าทำให้มีโอกาสที่จะเลือก action แบบสุ่มแทนที่จะเลือก action ที่ดีที่สุดมากกว่าสีชมพู

Recall: ϵ คือค่าความน่าจะเป็นที่จะเลือก action แบบสุ่ม แทนที่การเลือก action ที่มี Qt(a) มากที่สุด ซึ่ง reward จากการเลือก action ทั้งของสีฟ้าและสีชมพูนั้นแสดงในกราฟที่ 3 และ 4 ซึ่งจะเห็นได้ว่าหลังจาก timestep ที่ 170 เป็นต้นไปกราฟ reward ของสีชมพูแกว่งลงมาที่ reward ต่ำ ๆ น้อยกว่ากราฟสีฟ้า

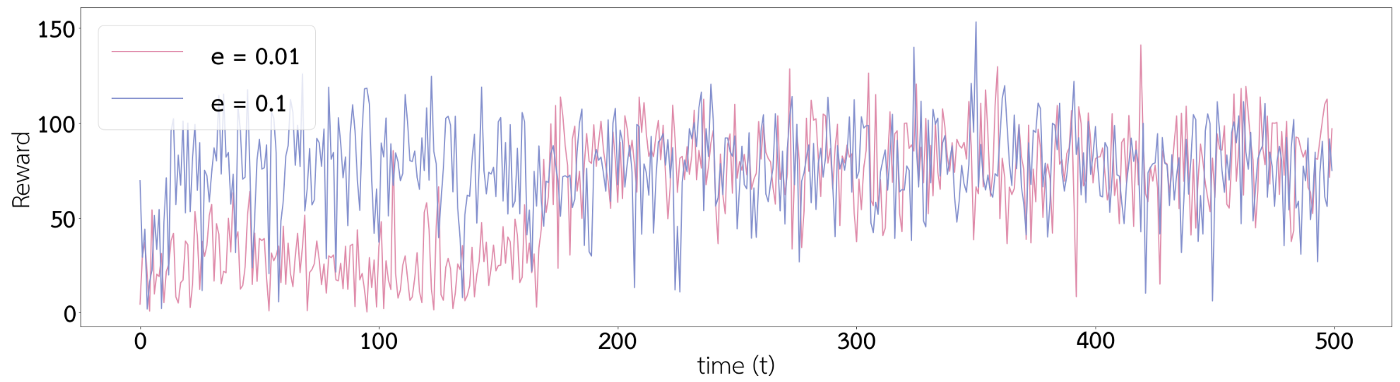
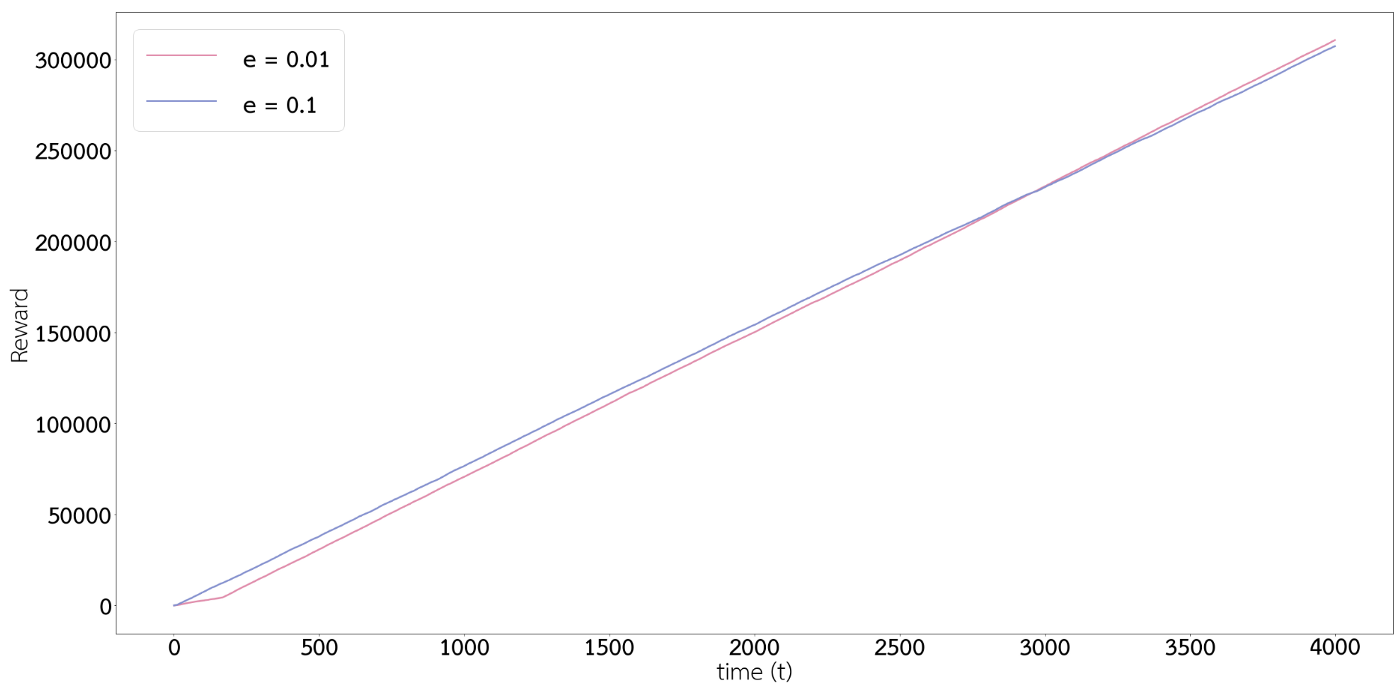
กราฟด้านล่างแสดง reward สะสมระหว่างสีฟ้ากับสีชมพู สังเกตในตอนแรกนั้น เส้นสีฟ้าอยู่เหนือเส้นสีชมพู นั่นเป็นเพราะว่าสีฟ้าค้นพบก่อนว่ากดตู้ 3 แล้วได้ reward มากที่สุด ทำให้สีฟ้าสะสม reward ในช่วงต้นได้มากกว่าสีชมพู แต่สีฟ้าดันไม่มีความ stable ในการเลือกตู้ 3 ได้เท่ากับสีชมพู เพราะมีค่า $\epsilon$ มากกว่า ทำให้สุดท้ายเส้นสีชมพูสามารถสะสม reward ได้มากกว่าสีฟ้า